|
|
|
|
|
Next: 3. First Order Equations |
|
This section will derive the solution of the Poisson equation in a
finite region as sketched in figure 2.9. The region will be
denoted as ![]() , and its boundary by
, and its boundary by ![]() . It will
again be assumed that the region is two-dimensional, leaving the
three-dimensional case to the homework. As shown in figure
2.9, inside the region the Poisson equation applies. In
case
. It will
again be assumed that the region is two-dimensional, leaving the
three-dimensional case to the homework. As shown in figure
2.9, inside the region the Poisson equation applies. In
case ![]() , this becomes the Laplace equation. On the boundary there
is some boundary condition that will for now be left arbitrary.
, this becomes the Laplace equation. On the boundary there
is some boundary condition that will for now be left arbitrary.
The big idea is to relate the finite domain solution to the infinite domain solution derived earlier.
![\begin{figure}
\begin{center}
\leavevmode
{}
\setlength{\unitlength}{1p...
...]{$\nabla^2 u_{\rm inf}\!=\!0$}}
\end{picture}
\end{center}
\end{figure}](img583.gif) |
For the given heat addition ![]() , you can still do the integral
, you can still do the integral
![]() over the domain
over the domain ![]() to get the infinite
domain solution. That solution will now be called
to get the infinite
domain solution. That solution will now be called ![]() , as
indicated in figure 2.10.
, as
indicated in figure 2.10.
The infinite domain solution satisfies the Poisson equation, but it does not satisfy the boundary conditions. It will turn out that some surface integrals must be added to it to get the boundary conditions right.
The precise form of these integrals can vary. The different versions
all give the same, correct, solution ![]() inside the domain
inside the domain ![]() .
However, they give different answers for the continuation of this
solution to outside the domain
.
However, they give different answers for the continuation of this
solution to outside the domain ![]() . So a meaningful
discussion of the various possibilities requires consideration of the
solution outside the domain. Even though the solution outside domain
. So a meaningful
discussion of the various possibilities requires consideration of the
solution outside the domain. Even though the solution outside domain
![]() is not actually a part of the problem.
is not actually a part of the problem.
The solution outside ![]() will be indicated as
will be indicated as ![]() , so
the picture becomes as shown in figure 2.10. Since you
surely do not want to just make up an arbitrary function
, so
the picture becomes as shown in figure 2.10. Since you
surely do not want to just make up an arbitrary function ![]() outside
outside
![]() , it will be assumed that
, it will be assumed that ![]() outside. So
outside. So ![]() satisfies the homogeneous Poisson equation, the Laplace equation. And
so does the infinite space solution
satisfies the homogeneous Poisson equation, the Laplace equation. And
so does the infinite space solution ![]() outside
outside ![]() ,
for that matter. Only integrating
,
for that matter. Only integrating ![]() over the domain
over the domain ![]() is the
same as setting
is the
same as setting ![]() to zero outside the domain.
to zero outside the domain.
(book, example 8.2)
The desired integral solution ![]() for the finite-region Poisson
solution is a generalization of the infinite domain solution
for the finite-region Poisson
solution is a generalization of the infinite domain solution
Since ![]() , the expression above represents an important
relationship between the infinite-domain solution
, the expression above represents an important
relationship between the infinite-domain solution ![]() and
the actual, finite-domain, solution
and
the actual, finite-domain, solution ![]() :
:
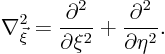
![\begin{figure}
\begin{center}
\leavevmode
{}
\setlength{\unitlength}{1p...
...\makebox(0,0)[l]{$u_{\rm out}$}}
\end{picture}
\end{center}
\end{figure}](img591.gif) |
Some caution is needed, however. The Green’s function is infinite
when
![]() , and integrals of infinite functions are not
proper. And neither are integrals over infinite regions. You must
exclude a very small circle around the point
, and integrals of infinite functions are not
proper. And neither are integrals over infinite regions. You must
exclude a very small circle around the point ![]() at which
at which
![]() is desired from the integration, and also the outside of
a very large circle, as indicated in figure 2.11. The
correct value for
is desired from the integration, and also the outside of
a very large circle, as indicated in figure 2.11. The
correct value for ![]() can then be obtained as the limit in
which the radius
can then be obtained as the limit in
which the radius ![]() of the small circle becomes zero and
the radius
of the small circle becomes zero and
the radius ![]() of the large circle becomes infinite. Also, you must
think of the integral as really consisting of two separate
integrations; one over the dark grey region
of the large circle becomes infinite. Also, you must
think of the integral as really consisting of two separate
integrations; one over the dark grey region ![]() and one over the
light grey exterior of
and one over the
light grey exterior of ![]() . The reason is that
. The reason is that ![]() and its
derivatives are not normally continuous on the surface
and its
derivatives are not normally continuous on the surface ![]() ,
and the divergence theorem can only be used for fairly smooth
functions.
,
and the divergence theorem can only be used for fairly smooth
functions.
To simplify the remaining discussion, the origin of the coordinate
system will be shifted towards the point ![]() at which
at which
![]() is desired. The integration coordinate
is desired. The integration coordinate ![]() can
then be described by polar coordinates
can
then be described by polar coordinates ![]() and
and ![]() centered
around this point. That simplifies the expression to be evaluated to
centered
around this point. That simplifies the expression to be evaluated to
To get a divergence integral, move a
![]() out in front,
adding a correction term to make up for the error in doing so:
out in front,
adding a correction term to make up for the error in doing so:
This final correction term, however, is zero. To see why, remember
that the Green’s function
![]() is the temperature
distribution due to a spike of heat at point
is the temperature
distribution due to a spike of heat at point ![]() . So
. So
![]() everywhere except at the singular point
everywhere except at the singular point
![]() . And since
. And since ![]() appears exactly the same way in
the Green’s function as
appears exactly the same way in
the Green’s function as ![]() , then so is
, then so is
![]() zero.
zero.
The remaining two terms become “surface” (actually,
contour in 2D,) integrals using the divergence theorem. In
particular:
To verify this expression, note that the “surfaces”
include the small and big circles, and that ![]() counts as
both part of the “surface” of the dark grey region in
figure 2.11 as well as part of the “surface” of
the light grey region. The normal vector
counts as
both part of the “surface” of the dark grey region in
figure 2.11 as well as part of the “surface” of
the light grey region. The normal vector ![]() on
on ![]() was taken to stick out of region
was taken to stick out of region ![]() , which accounts for the
additional minus sign in the corresponding
, which accounts for the
additional minus sign in the corresponding ![]() terms. Also
terms. Also
![]() is according to the total differential
of calculus the derivative
is according to the total differential
of calculus the derivative
![]() in the
direction normal to the surface. On the big circle, that is the same
as
in the
direction normal to the surface. On the big circle, that is the same
as
![]() , and on the small circle it is
, and on the small circle it is
![]() since there the outward normal points towards
the origin.
since there the outward normal points towards
the origin.
The second integral over the small circle is particularly interesting:
since
![]() , its
, its ![]() derivative is
derivative is ![]() , which
is the inverse of the “surface” (perimeter) of the
circle. So you get
, which
is the inverse of the “surface” (perimeter) of the
circle. So you get
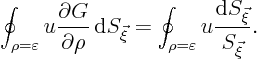
The first integral over the small circle in (2.9) is
vanishingly small and can be ignored. To see why, note that it is no
larger than the maximum value of the gradient of ![]() on the small
circle times
on the small
circle times
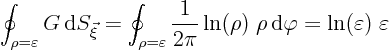
There is little that can be done about the integrals over
“surface” ![]() . However, the integrals over
the big circle in (2.9) still must be evaluated. To do
so, you must know something about the behavior of the solution
. However, the integrals over
the big circle in (2.9) still must be evaluated. To do
so, you must know something about the behavior of the solution
![]() for large values of
for large values of ![]() . In general, it is
described by
. In general, it is
described by
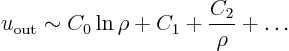
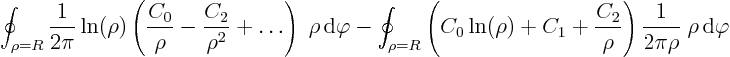
Collecting the results together, the solution for the temperature ![]() at any point
at any point ![]() is:
is:
Perform the equivalent analysis in the three dimensional case.
The previous subsection derived the solution to the Poisson equation in a finite domain. It was given by equation (2.10). This subsection will examine how this solution may be evaluated.
Except for
![]() , all other quantities in the right hand
side of equation (2.10) are evaluated at the point of
integration
, all other quantities in the right hand
side of equation (2.10) are evaluated at the point of
integration ![]() . For example,
. For example,
![]() stands for the normal derivative
stands for the normal derivative
![]() evaluated at
the boundary point
evaluated at
the boundary point ![]() of integration. That means that if you merely
know
of integration. That means that if you merely
know ![]() and the normal derivative
and the normal derivative
![]() on the
boundary, you can find
on the
boundary, you can find ![]() in the interior by taking
in the interior by taking ![]() to
be zero and doing the integrals above. Unfortunately, a priori at
most only one of
to
be zero and doing the integrals above. Unfortunately, a priori at
most only one of ![]() (Dirichlet boundary condition) or
(Dirichlet boundary condition) or
![]() (Neumann boundary condition) will be known on the
boundary.
(Neumann boundary condition) will be known on the
boundary.
Various solutions for this problem are possible. A panel method might
decide to compute the particular solution where ![]() is not
zero, but has the same values as
is not
zero, but has the same values as ![]() on the boundary. The big
advantage is then that the second integral in (2.10) drops
out, leaving only the last integral as a problem.
on the boundary. The big
advantage is then that the second integral in (2.10) drops
out, leaving only the last integral as a problem.
A simple panel method will now discretize the boundary in a large
number of densely spaced points, and then put a Green’s function
at each point. Since each Green’s function corresponds to the
addition of a spike of heat at that point, this is called a surface
“source” distribution. The problem remains that the
strengths
Alternatively, a panel method might decide to compute the solution for
the case that ![]() and
and ![]() have the same normal derivatives
on the boundary. That kills off the source integral, leaving the
second integral in (2.10). The quantity
have the same normal derivatives
on the boundary. That kills off the source integral, leaving the
second integral in (2.10). The quantity
![]() in this integral is called a
“dipole.” The reason for that name can be understood by
writing the definition of the derivative:
in this integral is called a
“dipole.” The reason for that name can be understood by
writing the definition of the derivative:
The previous subsection showed that the Poisson equation can be solved
by using suitable source and/or dipole distributions on the boundary
of the domain. However, the strengths of these distributions are not
usually known, since they involve both ![]() and its normal derivative
on the boundary, and there is only one boundary condition. And if an
exterior solution
and its normal derivative
on the boundary, and there is only one boundary condition. And if an
exterior solution ![]() is chosen to eliminate one of them,
that has the effect of introducing the unknown values of
is chosen to eliminate one of them,
that has the effect of introducing the unknown values of ![]() or its derivative into the problem. So at least one distribution
strength must be found using brute numerical force. Or by brute
analytical force, maybe, if the domain is simple.
or its derivative into the problem. So at least one distribution
strength must be found using brute numerical force. Or by brute
analytical force, maybe, if the domain is simple.
There is an exception, however, and it occurs for the Dirichlet problem inside a ball (a circle in two dimensions, a sphere in three-dimensions, etcetera.) In that case, suitable distribution strengths can be found by simple means.
The following discussion will restrict itself to the Laplace equation,
since the Poisson equation can always be turned into the Laplace
equation by subtracting the unbounded space solution ![]() .
This only produces an unimportant change in the inhomogeneous term of
the boundary condition. The problem to be solved is then:
.
This only produces an unimportant change in the inhomogeneous term of
the boundary condition. The problem to be solved is then:
In two dimensions, using polar coordinates, the solution is
This subsection will derive the two-dimensional formula above, leaving
the three-dimensional one for the homework. For simplicity, from now
on it will be assumed that the ball (i.e. circle in two-dimensions)
has unit radius,
The integral formula can be derived by a clever selection for the
solution ![]() outside the circle in the integral solution
(2.10). In particular, the trick is to take
outside the circle in the integral solution
(2.10). In particular, the trick is to take
The first thing to show is that ![]() satisfies the Laplace
equation. The integral solution (2.10) does not apply
otherwise. The Laplacian,
satisfies the Laplace
equation. The integral solution (2.10) does not apply
otherwise. The Laplacian,
To show that this is so, first differentiate (2.14) once,
using the chain rule to convert the ![]() derivatives of
derivatives of ![]() to
to
![]() derivatives:
derivatives:
![\begin{displaymath}
\nabla^2 u_{\rm out} = A \frac{1}{r^4}
\left[
\frac{\p...
... r}
+ r^2 \frac{\partial^2 u}{\partial \theta^2}
\right]
\end{displaymath}](img645.gif)
Now the idea is to try to choose the constant ![]() so that the integral
solution (2.10) only involves the given values of
so that the integral
solution (2.10) only involves the given values of ![]() on
the boundary. In particular, the normal derivative of
on
the boundary. In particular, the normal derivative of
![]() must be eliminated. Now for a spherical boundary, the
normal derivative is the radial derivative. And on the surface of the
ball,
must be eliminated. Now for a spherical boundary, the
normal derivative is the radial derivative. And on the surface of the
ball, ![]() . So on the boundary, using the expressions above,
. So on the boundary, using the expressions above,
For
![]() to vanish on the surface of
the sphere. according to the above equations you need to take
to vanish on the surface of
the sphere. according to the above equations you need to take ![]() .
In that case,
.
In that case,
![]() on the sphere equals
on the sphere equals ![]() , and
, and ![]() is
the given function
is
the given function ![]() on the surface of the sphere. So the integral
solution (2.10) becomes
on the surface of the sphere. So the integral
solution (2.10) becomes
The above solution ![]() is completely in terms of the given
function
is completely in terms of the given
function ![]() . So the Dirichlet problem has been solved.
. So the Dirichlet problem has been solved.
But of course you want to clean it up. You would like the solution of
a problem in a circle to be in terms of polar coordinates. So set
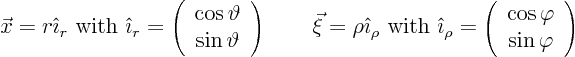
Also, the derivative
![]() normal to the
circle is simply
normal to the
circle is simply
![]() . G is a function of the
distance
. G is a function of the
distance
![]() between the points
between the points ![]() and
and
![]() ; in particular
; in particular ![]() in two dimensions. You can
write
in two dimensions. You can
write
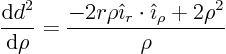
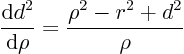
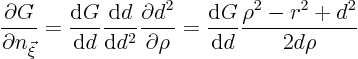
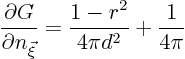
Plug that into the integral expression (2.15) for
![]() , taking
, taking ![]() from (2.16) with
from (2.16) with
![]() equal to
equal to
![]() , to get
, to get
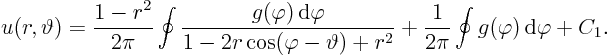
The two final terms are just constants, and they cancel each other.
The reason is that
Also, to allow for the case that the radial coordinate ![]() is not
normalized with the circle radius
is not
normalized with the circle radius ![]() , you want to replace
, you want to replace ![]() in the
above result with
in the
above result with ![]() . That produces the Poisson integral as stated
in the previous subsection.
. That produces the Poisson integral as stated
in the previous subsection.
Find a suitable solution ![]() outside the sphere in three dimensions. Show that it satisfies the Laplace equation.
outside the sphere in three dimensions. Show that it satisfies the Laplace equation.
Derive the Poisson integral formula in three dimensions as given in the previous subsection.
The Neumann problem in two dimensions is:
The derivation of the formula above is similar to the one in the
previous subsection. You will be disappointed to learn that you must
miss doing it in the homework. The same story does not work in three
dimensions since you cannot get rid of the unknown surface values of
![]() in both the source and dipole distributions. In two dimensions,
however, if you take
in both the source and dipole distributions. In two dimensions,
however, if you take
![]() , the
dipole strength is zero and only the source integral remains:
, the
dipole strength is zero and only the source integral remains:
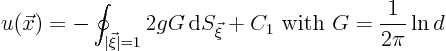
One important qualitative conclusion that can be drawn from the
various results of the previous subsections is that the solution of a
Laplace equation problem is infinitely smooth in the interior of the
region ![]() in which it applies.
in which it applies.
For example, consider the derived expression for ![]() if the exterior
solution is zero:
if the exterior
solution is zero:
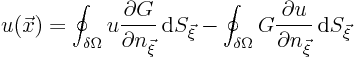 |
(2.18) |
So, if ![]() and
and
![]() are merely integrable on the
boundary, which still allows them to be quite singular, the solution
at every point in the interior will have infinitely many continuous
derivatives.
are merely integrable on the
boundary, which still allows them to be quite singular, the solution
at every point in the interior will have infinitely many continuous
derivatives.
It is somewhat different for the Poisson equation, since if the
forcing ![]() has a singularity at some point, then so will the solution
has a singularity at some point, then so will the solution
![]() . But still the solution for
. But still the solution for ![]() will be less singular than
will be less singular than ![]() is. For example, in two-dimensions a delta function in
is. For example, in two-dimensions a delta function in ![]() , whose
square is not integrable, produces a logarithmic Green‘s function,
for which every power is integrable over the singular point. In
general, it can be seen from Fourier solution of the Poisson problem
that
, whose
square is not integrable, produces a logarithmic Green‘s function,
for which every power is integrable over the singular point. In
general, it can be seen from Fourier solution of the Poisson problem
that ![]() will in general have two more square integrable derivatives
than
will in general have two more square integrable derivatives
than ![]() . (Assuming that lack of decay of
. (Assuming that lack of decay of ![]() at large distances is
not a factor or subtracted out first.)
at large distances is
not a factor or subtracted out first.)