| Partial Differential Equations Solution Manual |
|
© Leon van Dommelen |
|
Question:
Find a suitable solution 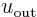 outside the sphere in three dimensions. Show that it satisfies the Laplace equation.
outside the sphere in three dimensions. Show that it satisfies the Laplace equation.
Answer:
In three dimensions, you will have to take
The Laplacian in spherical coordinates is readily available in table books. Taking derivatives goes in the same way as in two dimensions. However, note that you will need to use the product rule immediately.
![]() outside the sphere in three dimensions. Show that it satisfies the Laplace equation.
outside the sphere in three dimensions. Show that it satisfies the Laplace equation.