5.3 Understanding the Procedure

All the different steps in the separation of variable procedure as described may seem totally arbitrary. This section tries to explain why the steps are not arbitrary, but really quite logical. To understand this section does require that you have a good understanding of vectors and linear algebra. Otherwise you may as well skip this.

5.3.1 An ordinary differential equation as a model

Partial differential equations are relatively difficult to understand. Therefore we will instead consider an ordinary differential equation, but for a vector unknown:

$$\vec u_{tt} = - A \vec u$$

Here $A$ is some given constant matrix. The initial conditions are:

$$\vec u = \vec f, \quad \vec u_t = \vec g \qquad \mbox{at}\quad t=0$$

If you want to solve this problem, the trick is to write $\vec u$ in terms of the so-called eigenvectors of matrix $A$:

$$\vec u = u_1 \vec e_1 + u_2 \vec e_2 + u_3 \vec e_3 + \ldots$$

Here $u_1$, $u_2$, ...are numerical coefficients that will depend on time. Further $e_1$, $e_2$, ..., are the eigenvectors of matrix $A$. By definition, these satisfy

$$A \vec e_1 = \lambda_1 \vec e_1 \qquad A \vec e_2 = \lambda_2 \vec e_2 \qquad \ldots$$

where $\lambda_1$, $\lambda_2$, ...are numbers called the eigenvalues of matrix $A$. If $A$ is not a defective matrix, a complete set of independent eigenvectors will exist. That then means that the solution $\vec{u}$ of the problem can indeed be written as a combination of the eigenvectors. For simplicity, in this discussion it will be assumed that $A$ is not defective.

Now if you substitute the expression for $\vec{u}$ into the ordinary differential equation

$$\vec u_{tt} = - A \vec u$$

you get

$$\ddot u_1 \vec e_1 + \ddot u_2 \vec e_2 + \ldots = - \lambda_1 u_1 \vec e_1 + \lambda_2 u_2 \vec e_2$$

Here the dots in the left hand side indicate time derivatives. Also, in the right hand side, use was made of the fact that $A\vec{e}_i$ is the same as $\lambda_i\vec{e}_i$ for every value of $i=1,2,\ldots$.

The above equation can only be true if the coefficients of each individual eigenvector is the same in the left hand side as in the right hand side:

$$\ddot u_1 = - \lambda_1 u_1 \qquad \ddot u_2 = - \lambda_2 u_2 \qquad \ldots$$

That are ordinary differential equations. You can solve these particular ones relatively easily. However, each solution $u_1(t)$, $u_2(t)$, ...will have two integration constants that still remain unknown. To get them, use the initial conditions

$$\vec u = \vec f, \quad \vec u_t = \vec g \qquad \mbox{at}\quad t=0$$

where $\vec{f}$ and $\vec{g}$ are given vectors. You need to write these vectors also in terms of the eigenfunctions,

$$\vec f = f_1 \vec e_1 + f_2 \vec e_2 + \ldots \qquad \vec g = g_1 \vec e_1 + g_2 \vec e_2 + \ldots$$

Then you can see that what you need is

$$u_1(0) = f_1 \quad \dot u_1(0) = g_1 \qquad u_2(0) = f_2 \quad \dot u_2(0) = g_2 \qquad \ldots$$

That allows you to figure out the integration constants. So $u_1$, $u_2$, ...are now fully determined. And that means that the solution

$$\vec u = u_1 \vec e_1 + u_2 \vec e_2 + u_3 \vec e_3 + \ldots$$

is now fully determined. Just perform the summation at any time you want. So that is it.

The entire process becomes much easier if the matrix $A$ is what is called symmetric. For one, you do not have to worry about the matrix being defective. Symmetric matrices are never defective. Also, you do not have to worry about the eigenvalues possibly being complex numbers. The eigenvalues of a symmetric matrix are always real numbers.

And finally, the eigenvectors of a symmetric matrix can always be chosen to be unit vectors that are mutually orthogonal. In other words, they are like the unit vectors ${\hat\imath}'$, ${\hat\jmath}'$, ${\hat k}'$, ..., of a rotated Cartesian coordinate system.

The orthogonality helps greatly when you are trying to write $\vec{f}$ and $\vec{g}$ in terms of the eigenvectors. For example, you need to write $\vec{f}$ in the form

$$\vec f = f_1 \vec e_1 + f_2 \vec e_2 + \ldots$$

If the eigenvectors $\vec{e}_1$, $\vec{e}_1$, ..., are orthonormal, then $f_1$, $f_2$, ...can simply be found using dot products:

$$f_1 = \vec e_1 \cdot \vec f \qquad f_2 = \vec e_2 \cdot \vec f \qquad \ldots$$

Usually, however, you do not normalize the eigenvectors to length one. In that case, you can still write

$$\vec f = f_1 \vec e_1 + f_2 \vec e_2 + \ldots$$

but now you must find the coefficients as

$$f_1 = \frac{\vec e_1 \cdot \vec f}{\vec e_1 \cdot \vec e_1... ...\vec e_2 \cdot \vec f}{\vec e_2 \cdot \vec e_2} \qquad \ldots$$

In short you must divide by the square length of the eigenvector. The values for $g_1,g_2,\ldots$ can be found similarly.

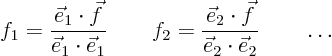
The next subsections will now show how all of the above carries over directly to the method of separation of variables for simple partial differential equations.

5.3.2 Vectors versus functions

The previous subsection showed how to solve an example ordinary differential for a vector unknown. The procedure had clear similarities to the separation of variables procedure that was used to solve the example partial differential equation in section 5.1.

However, in the ordinary differential equation, the unknown was a vector $\vec{u}$ at any given time $t$. In the partial differential equation, the unknown $u(x,t)$ was a function of $x$ at any given time. Also, the initial conditions for the ordinary differential equation were given vectors $\vec{f}$ and $\vec{g}$. For the partial differential equation, the initial conditions were given functions $f(x)$ and $g(x)$. The ordinary differential equation problem had eigenvectors $\vec{e}_1,\vec{e}_2,\ldots$. The partial differential equation problem had eigenfunctions $X_1(x),X_2(x),\ldots$.

The purpose of this subsection is to illustrate that it does not make that much of a difference. The differences between vectors and functions are not really as great as they may seem.

Let's start with a vector in two dimensions, like say the vector $\vec{v}=(3,4)$. You can represent this vector graphically as a point in a plane, but you can also represent it as the 'spike function', as in the left-hand sketch below:

$$\hbox{\epsffile{vecfun.eps}}$$

The first coefficient, $v_1$, is 3. That corresponds to a spike of height of 3 when the subscript, call it $i$, is 1. The second coefficient $v_2=4$, so there is a spike of height 4 at $i=2$. Similarly, the three-dimensional vector $\vec{v}=(3,4,2)$ can be graphed as the three-spike function in the middle figure. If you keep adding more dimensions, going to the limit of infinite-dimensional space, the spike graph $v_i$ approaches a function $f$ with a continuous coordinate $x$ instead of $i$.

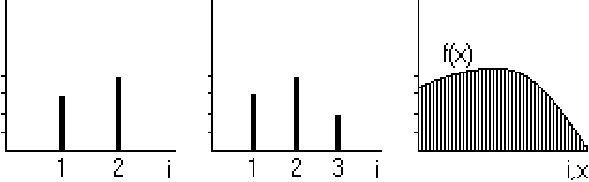
Phrased differently, you can think of a function $f(x)$ as an infinite column vector of numbers, with the numbers being the successive values of $f(x)$. In this way, vectors become functions. And vector analysis turns into functional analysis.

5.3.3 The inner product

You are not going to do much with vectors without the dot product. The dot product makes it possible to find the length of a vector, by multiplying the vector by itself and taking the square root. The dot product is also used to check if two vectors are orthogonal: if their dot product is zero, they are orthogonal. In this subsection, the dot product is generalized to functions.

The usual dot product of two arbitrary vectors $\vec f$ and $\vec g$ can be found by multiplying components with the same index $i$ together and summing that:

$$\vec f \cdot \vec g \equiv f_1 g_1 + f_2 g_2 + f_3 g_3$$

The below figure shows multiplied components using equal colors.

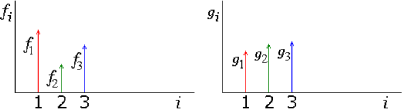
The three term sum above can be written more compactly as:

$$\vec f \cdot \vec g \equiv \sum_{\mbox{\scriptsize all }i} f_i g_i$$

The $\Sigma$ is called the “summation symbol.”

The dot (or “inner”) product of functions is defined in exactly the same way as for vectors, by multiplying values at the same $x$ position together and summing. But since there are infinitely many $x$-values, the sum becomes an integral:

$$(f,g) = \int_{\mbox{\scriptsize all }x} f(x) g(x) {\rm d} x$$ (5.1)

It is conventional to put a comma between the functions instead of a dot like for vectors. Also, people like to enclose the functions inside parentheses. But the idea is the same, as illustrated in the figure below:

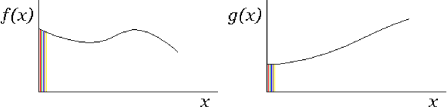
As an example, the ordinary differential equation model problem involved a given initial condition $\vec{f}$ for $\vec{u}$. To solve the problem, vector $\vec f$ had to be written in the form

$$\vec f = f_1 \vec e_1 + f_2 \vec e_2 + \ldots$$

Here the vectors $\vec{e}_1,\vec{e}_2,\ldots$ were the eigenvectors of the matrix $A$ in the problem. The coefficients $f_1,f_2,\ldots$ could be found using dot products:

$$f_1 = \frac{\vec e_1 \cdot \vec f}{\vec e_1 \cdot \vec e_1... ...\vec e_2 \cdot \vec f}{\vec e_2 \cdot \vec e_2} \qquad \ldots$$

This can be done this way as long as the eigenvectors are orthogonal. The dot product between any two different eigenvectors must be zero. The eigenvectors were indeed orthogonal, because it was assumed that the matrix $A$ in the problem was symmetric.

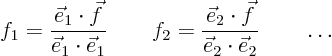
Similarly, the partial differential equation problem of section 5.1 involved a given initial condition $f(x)$ for $u(x,t)$. To solve the problem, this initial condition had to be written in the form:

$$f(x) = f_1 X_1(x) + f_2 X_2(x) + \ldots$$

Here $X_1(x),X_2(x),\ldots$ were the so-called eigenfunctions found in the separation of variables procedure. The coefficients $f_1,f_2,\ldots$ can be found using inner products

$$f_1 = \frac{(X_1,f)}{(X_1,X_1)} \qquad f_2 = \frac{(X_2,f)}{(X_2,X_2)} \qquad \ldots$$

This can be done this way as long as the eigenfunctions are orthogonal. The inner product between any two different eigenfunctions must be zero. The next section explains why that is indeed the case.

5.3.4 Matrices versus operators

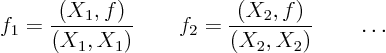
This section compares the solution procedure for the ordinary differential equation

$$\vec u_{tt} = - A \vec u \qquad \mbox{where $A$ is a matrix}$$

to that for the partial differential equation

$$u_{tt} = - L u \quad \mbox{where } L = - a^2 \frac{\partial^2}{\partial x^2}$$

You may wonder whether that makes any sense. A matrix is basically a table of numbers. The “linear operator” $L$ is shorthand for “take two derivatives and multiply the resulting function by the constant $-a^2$.”

But the difference between matrices and operators is not as great as it seems. One way of defining a matrix $A$ is as a thing that, given a vector $\vec{u}$, can produce a different vector $A\vec{u}$;

$$\vec u(t) \quad \begin{picture}(100,0) \put(50,11){\... ...t(0,2){\vector(1,0){100}} \end{picture} \quad A \vec u(t)$$

Similarly you can define an operator $L$ as a thing that, given a function $u$, produces another function $Lu$:

$$u(x,t) \quad \begin{picture}(100,10) \put(50,11){\ma... ...0){100}} \end{picture} \quad L u(x;t) = - a^2 u_{xx}(x,t)$$

After all, taking derivatives of functions simply produces another function. And multiplying a function by a constant simply produces another function.

Since it was already seen that vectors and functions are closely related, then so are matrices and operators.

Like matrices have eigenvectors, linear operators have eigenfunctions. In particular, section 5.1 found the appropriate eigenfunctions of the operator above to be

$$X_n = \cos\left(\frac{(2n-1) \pi x}{2\ell}\right) \qquad \mbox{for } n = 1, 2, 3, \ldots$$

(This also depended on the boundary conditions, but that point will be ignored for now.) You can check by differentiation that for these eigenfunctions

$$L X_n =- a^2 \frac{{\rm d}^2}{{\rm d}x^2} X_n = \lambda_n ... ...here } \lambda_n = a^2 \left(\frac{(2n-1)\pi}{2\ell}\right)^2$$

So they are indeed eigenfunctions of operator $L$.

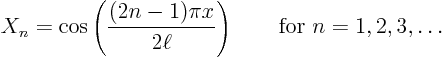
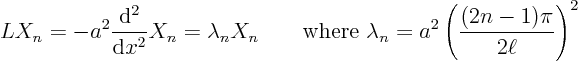
But, as the previous subsection pointed out, it was also assumed that these eigenfunctions are orthogonal. And that is not automatic. For a matrix the eigenvectors can be taken to be orthogonal if the matrix is symmetric. Similarly, for an operator the eigenfunctions can be taken to be orthogonal if the operator is symmetric.

But how do you check that for an operator? For a matrix, you simply write down the matrix as a table of numbers and check that the rows of the table are the same as the columns. You cannot do that with an operator. But there is another way. A matrix is also symmetric if for any two vectors $\vec{f}$ and $\vec{g}$,

$$\vec f \cdot(A\vec g) = (A\vec f) \cdot \vec g$$

In other words, symmetric matrices can be taken to the other side in a dot product. (In terms of linear algebra

$$\vec f \cdot(A\vec g) = \vec f^{ T} A \vec g \qquad (... ... \cdot \vec g = (A \vec f)^T \vec g = \vec f^{ T} A^T \vec g$$

where the superscript $T$ indicates transpose. For the two expression always to be the same requires $A=A^T$.)

Symmetry for operators can be checked similarly by whether they can be taken to the other side in inner products involving any two functions $f$ and $g$:

$$(f,Lg) = (Lf,g) \qquad \mbox{iff $L$ is symmetric.}$$

To check that for the operator above, write out the first inner product:

$$(f,Lg) = - a^2 \int_0^\ell f(x) g''(x) { \rm d}x$$

Now use integration by parts twice to get

$$(f,Lg) = - a^2 \int_0^\ell f''(x) g(x) { \rm d}x = (Lf,g)$$

So operator $L$ is symmetric and therefore it has orthogonal eigenfunctions. (It was assumed in the integrations by parts that the functions $f$ and $g$ satisfy the homogeneous boundary conditions at $x=0$ and $x=\ell$ given in section 5.1. All functions of interest here must satisfy them.)

5.3.5 Some limitations

Some limitations to the similarity between vectors and functions should be noted.

One difference is that the functions in partial differential equations must normally satisfy boundary conditions. The ones in the example problem were

$$u_x(0,t) = 0 \qquad u(\ell,t) = 0$$

Usually you do not have boundary conditions on vectors. But in principle you could create an analogue to the first boundary condition by demanding that the first component of vector $\vec{u}$ is the same as the second. An analogue to the second boundary condition would be that the very last component of vector $\vec u$ would be zero.

As long as matrix $A$ respects these boundary conditions, there is no problem with that. In terms of linear algebra, you would be working in a subspace of the complete vector space; the subspace of vectors that satisfy the boundary conditions.

There is another problem with the analogy between vectors and functions. Consider the initial condition $\vec{f}$ for the solution $\vec{u}$ of the ordinary differential equation. You can give the components of $\vec{f}$ completely arbitrary values and you will still get a solution for $\vec{u}$.

But now consider the initial condition $f(x)$ for the solution $u(x,t)$ of the ordinary differential equation. If you simply give a random value to the function $f$ at every individual value of $x$, then the function will not be differentiable. The partial differential equation for such a function will then make no sense at all. For functions to be meaningful in the solution of a partial differential equation, they must have enough smoothness that derivatives make some sense.

Note that this does not mean that the initial condition cannot have some singularities, like kinks or jumps, say. Normally, you are OK if the initial conditions can be approximated in a meaningful sense by a sum of the eigenfunctions of the problem. Because the functions that can be approximated in this way exclude the extremely singular ones, a partial differential equation will always work in a subspace of all possible functions. A subspace of reasonably smooth functions. Often when you see partial differential equations in literature, they also list the subspace in which it applies. That is beyond the scope of this book.