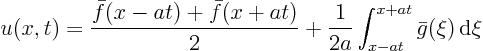5.2 Comparison with D'Alembert

The example problem of the previous section was also solved in chapter 4 using D'Alembert. It is interesting to compare the two solutions.

The separation of variables solution took the form:

$$u = \sum_{n=1}^\infty \left[ f_n \cos\frac{(2n-1)\pi... ...2n-1)\pi at}{2\ell} \right] \cos\frac{(2n-1)\pi x}{2\ell}$$

Some of its nice features are:

• It shows the natural frequencies (tones) to be $\pi a/2\ell$, $3 \pi a/2\ell$,...
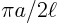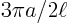• It shows the energy, so the strength, of each harmonic.
• The method is not restricted to the one-dimensional wave equation.

The D’Alembert solution took the form

$$u(x,t) = \frac{\bar f(x-at) + \bar f(x+at)}{2} + \frac{1}{2a} \int_{x-at}^{x+at} \bar g(\xi) { \rm d}\xi$$

Some of its nice features are

• The pressure can be evaluated at any point without doing infinite sums.
• It shows how wave fronts propagate.
• It shows regions of influence and dependence.

In short, each method has its advantages and disadvantages.