3.5 The inviscid Burgers’ equation

The inviscid Burgers’ equation is a model for nonlinear wave propagation, especially in fluid mechanics. It takes the form

$$\fbox{$\displaystyle u_t + u u_x = 0 $} %$$ (3.5)

The characteristic equations are, according to (3.4),

$$\frac{{\rm d}x}{{\rm d}t} = u \qquad \frac{{\rm d}u}{{\rm d}t} = 0.$$

The second of these shows that $u$ is constant along the characteristics of the Burgers’ equation, and then the first equation shows that the characteristic lines are straight lines in the $x,t$-plane.

The solution of the two characteristic ordinary differential equations above is simple:

$$x = u t + C_1 \qquad u = C_2$$

The general solution of the partial differential equation may be found in terms of $x$ and $t$ by noting that $C_2$ must be a function of $C_1$, $C_2=C_2(C_1)$, and then substituting $x-ut$ for $C_1$:

$$u = C_2(x-ut).$$

Some special cases are singular in those terms; they require that $C_1$ is written in terms of $C_2=u$:

$$x = u t + C_1(u).$$

Normally, either expression may be taken to be the general solution of the ordinary differential equation. One-parameter function $C_2$, respectively $C_1$ remains to be identified from whatever initial or boundary conditions there are.

3.5.1 Wave steepening

The given solution of the inviscid Burgers’ equation shows that the characteristics are straight lines. This is troubling, since straight lines are likely to intersect. In particular, since the point on a given characteristic lines propagates with speed $u$, faster points behind less fast ones will eventually overtake them.

As an example, consider the following problem:

$$u_t + u u_x = 0 \quad u(x,0) = 1 - \cos(x)$$

This problem is self-evidently periodic of period $2\pi$. Figure 3.4 shows how the characteristics intersect starting from time $t=1$.

Figure 3.4: Characteristics of Burgers’ equation for an example initial condition intersect for times greater than $t=1$.

Figure 3.5 shows profiles $u$ versus $x$ at various times. Note that for times greater than one, $u$ becomes a multiple-valued function. Physically, this is normally not acceptable: you can not have three different pressures or flow velocities at the same point.

Figure 3.5: Profiles at times $t = 0$, .5, 1, and 1.3 show wave steepening leading to a multiple-valued solution for times greater than $t=1$.

3.5.2 Shocks

The previous subsection noted that solutions of hyperbolic equations with intersecting characteristics are usually not physically acceptable. In fact, the desired solution for the inviscid Burgers’ equation is usually taken to be the solution of the viscous Burgers’ equation:

$$u_t + u u_x = \varepsilon u_{xx}$$

in the limit that the coefficient of viscosity $\varepsilon$ becomes zero.

Figure 3.6: Correct solution of Burgers’ equation for the same initial condition as the previous subsection.

Figure 3.7: Correct profiles for Burgers’ equation for the same initial condition as the previous subsection.

The viscous Burgers’ equation, too, is analytically solvable, though the solution will be skipped here. The bottom line is that it does not have multiple valued solutions. So what does the solution of the viscous Burgers’ equation look like in the limit that the viscosity becomes zero? Like figures 3.6 and 3.7. A jump discontinuity called a “shock” develops in $u$. The characteristics run into this shock and disappear.

The question now is of course, what determines the precise location of the shock? Clearly, it should be somewhere in the region of intersecting characteristics, but that still leaves a considerable uncertainty. Equations for the shock are needed. They usually follow from the requirement that certain quantities remain conserved in the solution. This is addressed in the next subsections.

3.5.3 Conservation laws

Often, partial differential equations express conservation of some physical quantity. For example, the continuity equation for the density of a fluid expresses conservation of mass of the fluid: the mass of a region of fluid is found by integrating the density over the volume of the region, and the continuity equation implies that mass is preserved in time.

The viscous Burgers’ equation, too, preserves some quantity. To see what, integrate the equation over an interval from some position $x=a$ to some position $x=b$:

$$\int_a^b u_t { \rm d}x + \int_a^b u u_x { \rm d}x = \varepsilon \int_a^b u_{xx} { \rm d}x$$

The last two integrals can be integrated after noting that $uu_x={\textstyle\frac{1}{2}}(u^2)_x$, to give

$$\int_a^b u_t { \rm d}x + {\textstyle\frac{1}{2}} u_b^2 - ... ...ac{1}{2}} u_a^2 = \varepsilon u_{x,b} - \varepsilon u_{x,a}$$

First consider the case that the problem is periodic and the integral is over a full period. Then the quantities at $a$ and $b$ are the same because of periodicity and drop away against each other. This shows that

$$\int_a^b u_t { \rm d}x = \frac{{\rm d}}{{\rm d}t} \int_a^b u { \rm d}x = 0$$

so that $\int u{ \rm d}x$ over a period is a conserved quantity, unchanging in time. The unknown $u$ itself can then be identified as the amount of conserved quantity per unit length.

Next consider the case that the region of integration is not a period. In that case, the Leibniz rule for differentiating integrals says that

$$\frac{{\rm d}}{{\rm d}t} \int_a^b u_t { \rm d}x = \int_a^... ...u_b \frac{{\rm d}b}{{\rm d}t} - u_a \frac{{\rm d}a}{{\rm d}t}$$

and plugging that into the integrated equation:

$$\frac{{\rm d}}{{\rm d}t} \int_a^b u_t { \rm d}x = \left... ...- {\textstyle\frac{1}{2}} u_a^2 + \varepsilon u_{x,a}\right).$$

Now think of interval $a,b$ as being preceded by a similar interval $a'b'$, with $b'=a$. It is evident from the above expression that the reduction in the value of $\int_a^bu{ \rm d}{x}$ caused by the term

$$\left(u_a \frac{{\rm d}a}{{\rm d}t} - {\textstyle\frac{1}{2}} u_a^2 + \varepsilon u_{x,a}\right)$$

is fully compensated for by a corresponding increase in $\int_{a'}^{b'}u{ \rm d}{x}$, because the same term shows up there as

$$\left(u_{b'} \frac{{\rm d}b'}{{\rm d}t} - {\textstyle\frac{1}{2}} u_{b'}^2 + \varepsilon u_{x,b'}\right)$$

with a plus sign. So whatever goes out of interval $ab$ at $a$ goes into interval $a'b'$. The same way, whatever comes in at $b$ comes out of the region $x>b$. It follows that $\int u { \rm d}x$ is still preserved.

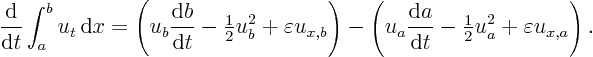
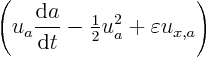
It may be noted that in

$$\left(u_b \frac{{\rm d}b}{{\rm d}t} - {\textstyle\frac{1}{2}} u_b^2 + \varepsilon u_{x,b}\right)$$

the first term represents the amount of conserved quantity being swept into the interval by the motion of its end point $b$. Typically, the second term physically corresponds to the amount of conserved quantity being convected out by motion of the substance, and the final term to the amount diffusing in by random molecular motion.

3.5.4 Shock relation

If the solution of the inviscid Burgers’ equation is indeed supposed to approximate the solution of the viscous equation when the coefficient of viscosity $\epsilon$ becomes zero, it puts a condition on how the shocks must move. The shock is vanishingly thin and can only hold a negligible amount of conserved material. So, whatever goes into the shock at one side must come out at the other side.

The amounts going in and out of a region were derived in the previous section for an interval $ab$. Taking point $a$ just before the shock and $b$ just behind the shock, so that to practical purposes $a=x_s=b$ with $x_s$ the shock velocity, equality of the amounts going in and out requires

$$u_b \frac{{\rm d}x_s}{{\rm d}t} - {\textstyle\frac{1}{2}} ... ...a \frac{{\rm d}x_s}{{\rm d}t} - {\textstyle\frac{1}{2}} u_a^2$$

Solving for the shock velocity ${\rm d}x_s/{\rm d}t$, you get

$$\frac{{\rm d}x_s}{{\rm d}t} = {\textstyle\frac{1}{2}} (u_b + u_a)$$

It follows that the shock must move with the average of the characteristic velocities $u_a$ and $u_a$ just before and after the shock. Figures 3.6 and 3.7 were obtained by finding the shock position from that relationship.

Shock relations, like this one for Burgers’ equation, are known as Rankine-Hugoniot relations in fluid mechanics. When deriving shock relations, make sure that the unknown variables are the conserved quantities per unit volume. If you multiply the inviscid Burgers’ equation by $2 u$, you get

$$(u^2)_t + 2 u^2 u_x = 0$$

from which it can be seen that as far as the inviscid Burgers’ equation is concerned, $\int u^2 { \rm d}x$ is also a conserved quantity. But the shocks you would compute using the corresponding conservation law are going to be different, and wrong if the true conserved quantity across shocks is the $\int u{ \rm d}x$ of the viscous Burgers’ equation.

Figure 3.8: Incorrect solution to Burgers’ equation for the initial pulse profile shown in the center graphic. The left shock violates the entropy condition.

Figure 3.9: Correct solution to Burgers’ equation for the initial pulse profile shown in the center graphic. The left shock has been replaced by an expansion fan.

3.5.5 The entropy condition

Consider now Burgers’ equation for a unit “pulse” initial condition:

$$u_t + u u_x = 0 \qquad u(x,0) = \left\{ \begin{array}{l}... ...e x \le 1 0 \mbox{ everywhere else} \end{array} \right.$$

This problem has a simple solution that is also quite wrong. It is shown in figure 3.8. It implies that the pulse moves with velocity $\frac12$ towards the right. Note that both shocks satisfy the shock condition of the previous section; $u=0$ at one side of each shock and $u=1$ at the other side average in each case to ${\rm d}{x}_s/{\rm d}{t}=\frac12$.

The problem is with the left shock. Characteristics should run into the shock for increasing time like for the right shock, not emerge out of it as happens for the left one. In fluid mechanics, the left shock is what is called an “expansion” shock. It produces an adiabatic decrease in entropy over the shock, something the second law of thermodynamics does not allow. For that reason, the condition that characteristics must run into the shock is called the “entropy condition.”

The correct solution is shown in figure 3.9. The left jump in the initial condition spreads out into what is called an “expansion far.” Unlike the shock, the expansion fan is a perfectly good nonsingular solution of the Burgers“ equation, though you must use the solution form $x=ut+C_1(u)$ with $C_1=0$. The solution form $u=C_2(x-ut)$ does not work since $x-ut$ is the same, zero, on all characteristics, and u must be different on different characteristics. Conversely, in the other three regions, you must use the solution form $u=C_2(x-ut)$ with $C_2$ either uniformly zero or uniformly one. There the solution form $x=ut+C_1(u)$ does not work since $u$ is the same for all characteristics and $x-ut$ is not.

It may also be observed that the entropy condition is necessary to get a unique solution; both figures 3.8 and 3.9 satisfy the Burgers“ equation at all continuous points and the shock conditions at all discontinuities.