3.1 Classification and characteristics

The general quasi-linear first order equation in two dimensions takes the form

$$\fbox{$\displaystyle a u_x + b u_y = c $} %$$ (3.1)

where $a$, $b$, and $c$ may depend on $x$, $y$, and $u$. All scalar first order equation are classified as hyperbolic equations.

The characteristics are defined by

$$\fbox{$\displaystyle \frac{{\rm d}y}{{\rm d}x} = \frac{b}{a} $} %$$ (3.2)

They will form a single family of lines in the $x,y$-plane. (In contrast, the characteristics of scalar second order hyperbolic differential equations form two intersecting families of lines.)

In general, the variation of a function $u$ of two variables along a line is given by the total differential of calculus,

$$\frac{{\rm d}u}{{\rm d}x} = u_x + u_y \frac{{\rm d}y}{{\rm d}x}$$

but along the characteristic lines that becomes

$$\frac{{\rm d}u}{{\rm d}x} = u_x + u_y \frac{b}{a}$$

and comparing with the partial differential equation, it is seen that the right hand side is $c/a$. So the variation of the solution $u$ along the characteristic lines is given by

$$\fbox{$\displaystyle \frac{{\rm d}u}{{\rm d}x} = \frac{c}{a} $} %$$ (3.3)

Note that frequently, you may have to solve the ordinary differential equations in a different form or order. For example, if $b/a$ depends on $u$, you will not be able to solve ${\rm d}{y}/{\rm d}{x}=b/a$ to find $y$ as a function of $x$ since $u$ in $b/a$ is still an unknown function of $x$. But maybe, say, $c/b$ is not a function of $x$, in which case you could solve ${\rm d}{u}/{\rm d}{y}=c/b$; then you could plug that solution for $u$ as a function of $y$ into ${\rm d}{x}/{\rm d}{y}=a/b$ to get an equation for $x$ that no longer involves $u$. The bottom line is that it is really best to write the characteristic equations as

$$\fbox{$\displaystyle {\rm d}x : {\rm d}y : {\rm d}u = a : b : c $} %$$ (3.4)

and pick from those proportionalities the ratio that is easiest to solve first.

In all the unsolved problems in the book, there is at least one solvable ratio. But if there is none, you may be forced to try to change variables, e.g. to polar, or eliminate one variable by, say, differentiating a ratio, hopefully producing a second order ordinary differential equation with one variable eliminated.

Example

Question: (5.30) Solve

$$y u_x + x u_y = cu$$

Solution:

This example wants to solve the partial differential equation

$$y u_x + x u_y = cu$$

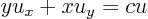
For this equation, a ratio like ${\rm d}{u}/{\rm d}{x}=cu/y$ is not immediately solvable for $u$, since $y$ besides $u$ would be an unknown function of $x$. The only solvable ratio is in fact that between ${\rm d}{x}$ and ${\rm d}{y}$:

$$\frac{{\rm d}y}{{\rm d}x} = \frac{x}{y} \qquad\Rightarro... ...y = x { \rm d}x \qquad\Rightarrow\qquad y^2 = x^2 + C_1$$

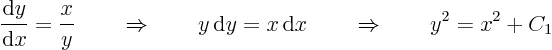
where $C_1$ is the integration constant. These characteristic lines are hyperbola; they are sketched in figure 3.1.

Figure 3.1: Characteristics of the partial differential equation of problem 5.30.

Now that $y$ is a known function of $x$, specifically $y=\sqrt{x^2+C_1}$ assuming it is positive, the ordinary differential equation for $u$ can be solved

$$\frac{{\rm d}u}{{\rm d}x} = \frac{cu}{y} = \frac{cu}{\sqrt{x^2+C_1}}$$

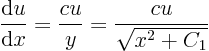
to give

$$\frac{{\rm d}u}{u} = c \frac{{\rm d}x}{\sqrt{x^2+C_1}} \... ...t = c \ln\left(x + \sqrt{x^2+C_1}\right) + \ln\vert C_2\vert$$

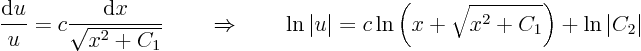
Taking exponentials and noting that the square root equals $y$, this simplifies to

$$u = C_2 (x+y)^c \qquad\mbox{along a characteristic}\qquad y^2 = x^2 + C_1$$

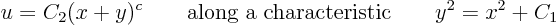
For example, if it is given that $u=1$ at the point $x=y=1$ shown as a fat dot in figure 3.2, then it follows from the above general expressions that $C_1=0$, so the characteristic line is the line $y=x$ shown in grey, and that $C_2=1/2^c$, so you would get $u(x,x) = x^c$ for $u$ on the grey line.

Figure 3.2: Given the value of $u$ at a single point on a characteristic line, $u$ can be found at every point on that line.

Example

Question: (5.6) Solve the nasty example

$$x u_x + y u u_y = -xy.$$

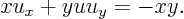
Solution:

In this case, none of the ratios

$$\frac{{\rm d}y}{{\rm d}x}=\frac{uy}{x} \qquad \frac{{\... ...m d}x}=-y \qquad \frac{{\rm d}u}{{\rm d}y}=-\frac{x}{u}$$

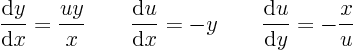
is a solvable ordinary differential equation; each involves three variables. You might try to take a derivative of an equation, like

$$\frac{{\rm d}^2 u}{{\rm d}x^2} = - \frac{{\rm d}y}{{\rm ... ...}^2 u}{{\rm d}x^2} = \frac{u}{x} \frac{{\rm d}u}{{\rm d}x}$$

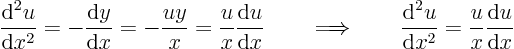
which is indeed an ordinary differential equation for $u(x)$ not involving the unknown $y$. But it is an awkward second order nonlinear equation.

The trick is to guess that the combination $xy$ can be found as a function of $u$:

$$y \frac{{\rm d}x}{{\rm d}u} + x \frac{{\rm d}y}{{\rm d}u} ... ...\Longrightarrow\qquad \frac{{\rm d}xy}{{\rm d}u} = - 1 - u$$

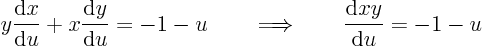
which produces

$$xy = - u - {\textstyle\frac12}u^2 + C_1.$$

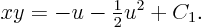
This can then be plugged into

$$\frac{{\rm d}x}{{\rm d}u} = - \frac{1}{y} = - \frac{x}{xy} = \frac{x}{u + {\textstyle\frac12}u^2 - C_1}$$

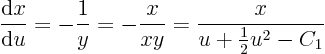
to get a separable equation giving $x$ as a function of $u$, with another integration constant $C_2$. However, that becomes a mess, involving either an arctan or logarithm, depending on the value of $C_1$.