8.4 A story by Wheeler

Con­sider a sim­ple ques­tion. Why are all elec­trons so ab­solutely equal? Would it not be a lot less bor­ing if they had a range of masses and charges? As in “I found a re­ally big elec­tron this morn­ing, with an un­be­liev­able charge!” It does not hap­pen.

And it is in fact far, far, worse than that. In quan­tum me­chan­ics elec­trons are ab­solutely iden­ti­cal. If you re­ally write the cor­rect (clas­si­cal) wave func­tion for an hy­dro­gen atom fol­low­ing the rules of quan­tum me­chan­ics, then in prin­ci­ple you must in­clude every elec­tron in the uni­verse as be­ing present, in part, on the atom. Elec­trons are so equal that one can­not be present on a hy­dro­gen atom un­less every elec­tron in the uni­verse is.

There is a sim­ple ex­pla­na­tion that the fa­mous physi­cist Wheeler gave to his tal­ented grad­u­ate stu­dent Richard Feyn­man. In Feyn­man’s words:

“As a by-prod­uct of this same view, I re­ceived a tele­phone call one day at the grad­u­ate col­lege at Prince­ton from Pro­fes­sor Wheeler, in which he said, ‘Feyn­man, I know why all elec­trons have the same charge and the same mass’ Why? Be­cause, they are all the same elec­tron! And, then he ex­plained on the tele­phone, ...” [Richard P. Feyn­man (1965) No­bel prize lec­ture. [[5]]]

Fig­ure 8.5: The space-time di­a­gram of Wheeler’s sin­gle elec­tron.

What Pro­fes­sor Wheeler ex­plained on the phone is sketched in the space-time di­a­gram fig­ure 8.5. The world-line of the only elec­tron there is is con­stantly trav­el­ing back and for­wards be­tween the past and the fu­ture. At any given time, like to­day, this sin­gle elec­tron can be ob­served at count­less dif­fer­ent lo­ca­tions. At the lo­ca­tions where the elec­tron is trav­el­ing to the fu­ture it be­haves like a nor­mal elec­tron. And Wheeler rec­og­nized that where the elec­tron is trav­el­ing to­wards the past, it be­haves like a pos­i­tively charged elec­tron, called a positron. The mys­tery of all those count­less iden­ti­cal elec­trons was ex­plained.

What had Feyn­man to say about that!? Again in his words:

“ But, Pro­fes­sor, I said, ‘there aren't as many positrons as elec­trons.’ ‘Well, maybe they are hid­den in the pro­tons or some­thing,’ he said. I did not take the idea that all the elec­trons were the same one from him as se­ri­ously as I took the ob­ser­va­tion that positrons could sim­ply be rep­re­sented as elec­trons go­ing from the fu­ture to the past in a back sec­tion of their world lines. That, I stole!” [Richard P. Feyn­man (1965) No­bel prize lec­ture. [[5]]]

And there are other prob­lems, like that elec­trons can be cre­ated or de­stroyed in weak in­ter­ac­tions.

But with­out doubt, if this was art in­stead of quan­tum me­chan­ics, Wheeler’s pro­posal would be con­sid­ered one of the great­est works of all time. It is stun­ning in both its ut­ter sim­plic­ity and its in­con­ceiv­able scope.

There is a place for es­thet­ics in quan­tum me­chan­ics, as the Dirac equa­tion il­lus­trates. There­fore this sec­tion will take a very bi­ased look at whether the idea is re­ally so truly in­con­ceiv­able as it might ap­pear. To do so, only positrons and elec­trons will be con­sid­ered, with their at­ten­dant pho­tons. Shape-shift­ing elec­trons are a ma­jor ad­di­tional com­pli­ca­tion. And re­call clas­si­cal me­chan­ics. Some of the most es­thet­i­cal re­sults of clas­si­cal me­chan­ics are the laws of con­ser­va­tion of en­ergy and mo­men­tum. Rel­a­tiv­ity and then quan­tum me­chan­ics even­tu­ally found that clas­si­cal me­chan­ics is fun­da­men­tally com­pletely wrong. But did con­ser­va­tion of en­ergy and mo­men­tum dis­ap­pear? Quite the con­trary. They took on an even deeper and more es­thet­i­cally grat­i­fy­ing role in those the­o­ries.

With other par­ti­cles shoved out of the way, the ob­vi­ous ques­tion is the one of Feyn­man. Where are all the positrons? One idea is that they ended up in some other part of space. But that seems to be hard to rec­on­cile with the fact that space seems quite sim­i­lar in all di­rec­tions. The positrons will still have to be around us. So why do we not see them? Re­call that the model con­sid­ered here has no pro­tons for positrons to hide in.

Ob­vi­ously, if the positrons have nowhere to hide, they must be in plain view. That seems the­o­ret­i­cally pos­si­ble if it is as­sumed that the positron quan­tum wave func­tions are de­lo­cal­ized on a gi­gan­tic scale. Note that as­tron­omy is short of a large amount of mass in the uni­verse one way or the other. De­lo­cal­ized an­ti­mat­ter to the tune of the vis­i­ble mat­ter would be just a drop in the bucket.

A bit of math­e­mat­i­cal trick­ery called the Cauchy-Schwartz in­equal­ity can be used to il­lus­trate the idea. Con­sider a uni­verse of vol­ume ${\cal V}$. For sim­plic­ity, as­sume that there is just one elec­tron and one positron in this uni­verse. More does not seem to make a fun­da­men­tal dif­fer­ence, at least not in a sim­plis­tic model. The elec­tron has wave func­tion $\psi_1$ and the positron $\psi_2$. The Cauchy-Schwartz in­equal­ity says that:

$$\left\vert\int_{\cal V}\psi_1^*\psi_2{ \rm d}^2{\skew0\vec... ... r}\int_{\cal V}\vert\psi_2\vert^2{ \rm d}^2{\skew0\vec r}= 1$$

Take the left hand side as rep­re­sen­ta­tive for the in­ter­ac­tion rate be­tween elec­trons and positrons. Then if the wave func­tions of both elec­trons and positrons are com­pletely de­lo­cal­ized, the in­ter­ac­tion rate is 1. How­ever, if only the positrons are com­pletely de­lo­cal­ized, it is much smaller. Sup­pose the elec­tron is lo­cal­ized within a vol­ume $\varepsilon{\cal V}$ with $\varepsilon$ a very small num­ber. Then the in­ter­ac­tion rate is re­duced from 1 to $\varepsilon$. If both elec­trons and positrons are lo­cal­ized within vol­umes of size $\varepsilon{\cal V}$ it gets messier. If the elec­tron and positron move com­pletely ran­domly and quickly through the vol­ume, the av­er­age in­ter­ac­tion rate would still be $\varepsilon$. But elec­trons and positrons at­tract each other through their elec­tric charges, and on a large scale also through grav­ity. That could in­crease the in­ter­ac­tion rate greatly.

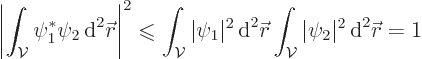
The ob­vi­ous next ques­tion is then, how come that positrons are de­lo­cal­ized and elec­trons are not? The sim­ple an­swer to that is: be­cause elec­trons come to us from the com­pact Big Bang stages of the uni­verse. The positrons come to us from the fi­nal stages of the evo­lu­tion of the uni­verse where it has ex­panded be­yond limit.

Un­for­tu­nately, that an­swer, while sim­ple, is not sat­is­fac­tory. Mo­tion in quan­tum me­chan­ics is es­sen­tially time re­versible. And that means that you should be able to ex­plain the evo­lu­tion of both elec­trons and positrons com­ing out of the ini­tial Big Bang uni­verse. Go­ing for­ward in time.

A more rea­son­able idea is that the other op­tions do not pro­duce sta­ble sit­u­a­tions. Con­sider a lo­cal­ized positron in an early uni­verse that by ran­dom chance hap­pens to have more lo­cal­ized elec­trons than positrons. Be­cause of at­trac­tion ef­fects, such a positron is likely to find a lo­cal­ized elec­tron to an­ni­hi­late with. That is one less lo­cal­ized positron out of an al­ready re­duced pop­u­la­tion. A de­lo­cal­ized positron could in­ter­act sim­i­larly with a de­lo­cal­ized elec­tron, but there are less of these. The re­verse sit­u­a­tion holds for elec­trons. So you could imag­ine a run­away process where the positron pop­u­la­tion evolves to de­lo­cal­ized states and the elec­trons to lo­cal­ized ones.

An­other way to look at it is to con­sider how wave func­tions get lo­cal­ized in the first place. The wave func­tion of a lo­cal­ized iso­lated par­ti­cle wants to dis­perse out over time. Cos­mic ex­pan­sion would only add to that. In the or­tho­dox view, par­ti­cles get lo­cal­ized be­cause they are mea­sured. The ba­sics of this process, as de­scribed by an­other grad­u­ate stu­dent of Wheeler, Everett III, are in sec­tion 8.6. Un­for­tu­nately, the process re­mains poorly un­der­stood. But sup­pose, say, that mat­ter lo­cal­izes mat­ter but de­lo­cal­izes an­ti­mat­ter, and vice-versa. In that case a slight dom­i­nance of mat­ter over an­ti­mat­ter could con­ceiv­ably lead to a run-away sit­u­a­tion where the mat­ter gets lo­cal­ized and the an­ti­mat­ter de­lo­cal­ized.

Among all the ex­otic sources that have been pro­posed for the dark mat­ter in the uni­verse, de­lo­cal­ized an­ti­mat­ter does not seem to get men­tioned. So prob­a­bly some­one has al­ready solidly shown that it is im­pos­si­ble.

But that does not in­val­i­date Wheeler’s ba­sic idea, of course. As Wheeler him­self sug­gested, the positrons could in fact be hid­ing in­side the pro­tons through the weak-force mech­a­nism. Then of course, you need to ex­plain how the positrons came to be hid­ing in­side the pro­tons. Why not the elec­trons in­side the an­tipro­tons? That would be messier, but it does not mean it could not be true. In fact, it is one of the sur­prises of ad­vanced par­ti­cle physics that the en­tire lep­ton-quark fam­ily seems to be one in­sep­a­ra­ble multi-com­po­nent par­ti­cle, [27, p. 210]. It seems only fair to say that Wheeler’s idea pre­dicted this. For clearly, the elec­tron could not main­tain its un­mutable iden­tity if re­peat­edly changed into par­ti­cles with a sep­a­rate and in­de­pen­dent iden­tity. So Wheeler’s idea may not be so crazy af­ter all, look­ing at the facts. It pro­vides a real ex­pla­na­tion why iden­ti­cal par­ti­cles are so per­fectly iden­ti­cal. And it pre­dicted some­thing that would only be ob­served well into the fu­ture.

Still, the bot­tom line re­mains the beauty of the idea. As the math­e­mati­cian Weyl noted, un­fazed af­ter Ein­stein shot down an idea of his:

“When there is a con­flict be­tween beauty and truth, I choose beauty.”