| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.49 The generalized variational principle
The purpose of this note is to verify directly that the variation of
the expectation energy is zero at any energy eigenstate, not just the
ground state.
Suppose that you are trying to find some energy eigenstate 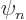 with eigenvalue
with eigenvalue 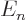 , and that you are close to it, but no
cigar. Then the wave function can be written as
, and that you are close to it, but no
cigar. Then the wave function can be written as
where 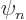 is the one you want and the remaining terms together
are the small error in wave function, written in terms of the
eigenfunctions. Their coefficients
is the one you want and the remaining terms together
are the small error in wave function, written in terms of the
eigenfunctions. Their coefficients
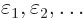 are small.
are small.
The normalization condition 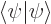
 1 is, using
orthonormality:
1 is, using
orthonormality:
The expectation energy is
or plugging in the normalization condition to eliminate
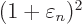
Assuming that the energy eigenvalues are arranged in increasing order,
the terms before 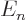 in this sum are negative and the ones behind
in this sum are negative and the ones behind
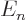 positive. So
positive. So 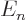 is neither a maximum nor a minimum;
depending on conditions
is neither a maximum nor a minimum;
depending on conditions 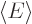 can be greater or smaller than
can be greater or smaller than
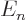 .
.
Now, if you make small changes in the wave function, the values of
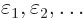 will slightly change, by small
amounts that will be indicated by
will slightly change, by small
amounts that will be indicated by
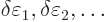 , and you get
, and you get
This is zero when 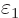


 0, so when
0, so when  is the exact eigenfunction
is the exact eigenfunction 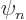 .
And it is nonzero as soon as any of
.
And it is nonzero as soon as any of
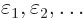 is nonzero; a change in that
coefficient will produce a nonzero change in expectation energy. So
the variational condition
is nonzero; a change in that
coefficient will produce a nonzero change in expectation energy. So
the variational condition 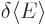
 0 is
satisfied at the exact eigenfunction
0 is
satisfied at the exact eigenfunction 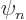 , but not at any
nearby different wave functions.
, but not at any
nearby different wave functions.
The bottom line is that if you locate the nearest wave function for
which 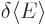
 0 for all acceptable small changes in
that wave function, well, if you are in the vicinity of an energy
eigenfunction, you are going to find that eigenfunction.
0 for all acceptable small changes in
that wave function, well, if you are in the vicinity of an energy
eigenfunction, you are going to find that eigenfunction.
One final note. If you look at the expression above, it seems like
none of the other eigenfunctions are eigenfunctions. For example, the
ground state would be the case that 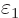 is one, and all
the other coefficients zero. So a small change in
is one, and all
the other coefficients zero. So a small change in 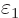 would seem to produce a change
would seem to produce a change 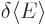 in
expectation energy, and the expectation energy is supposed to be
constant at eigenstates.
in
expectation energy, and the expectation energy is supposed to be
constant at eigenstates.
The problem is the normalization condition, whose differential form
says that
At 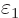
 1 and
1 and 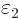

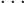

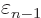

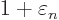

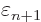

 0, this implies that the change
0, this implies that the change
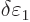 must be zero. And that means that the change in
expectation energy is in fact zero. You see that you really need to
eliminate
must be zero. And that means that the change in
expectation energy is in fact zero. You see that you really need to
eliminate 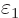 from the list of coefficients near
from the list of coefficients near
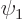 , rather than
, rather than 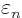 as the analysis for
as the analysis for
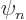 did, for the mathematics not to blow up. A coefficient that
is not allowed to change at a point in the vicinity of interest is a
confusing coefficient to work with.
did, for the mathematics not to blow up. A coefficient that
is not allowed to change at a point in the vicinity of interest is a
confusing coefficient to work with.
![]()
![]() ,
,![]()
![]()
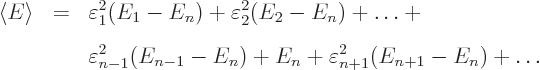
![]()
![]() ,
,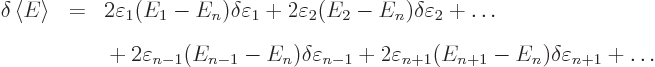
![]()
![]()
![]()
![]()
![]()