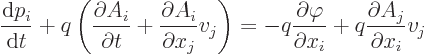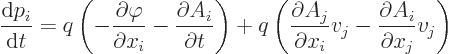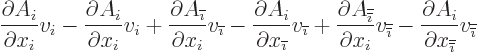| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.6 Lorentz force derivation
To derive the given Lorentz force from the given Lagrangian, plug the
canonical momentum and the Lagrangian into the Lagrangian equation of
motion. That gives
This uses the Einstein convention that summation over  is to be
understood. Reorder to get
is to be
understood. Reorder to get
The first parenthetical expression is the electric field as claimed.
The quantity in the second parenthetical expression may be rewritten by
expanding out the sums over  to give
to give
where 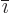 follows
follows  in the cyclic sequence
in the cyclic sequence
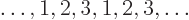 and
and 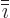 precedes it. The first two
terms drop out and the others can be recognized as component number
precedes it. The first two
terms drop out and the others can be recognized as component number
 of
of 

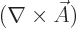 . (For example,
just write out the first component of
. (For example,
just write out the first component of 

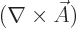 and compare it the expression above for
and compare it the expression above for 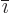
 2 and
2 and 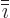
 3.) Defining
3.) Defining 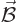 as
as 

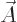 , the Lorentz force law results.
, the Lorentz force law results.