D.4 Lorentz trans­for­ma­tion de­riva­tion

This note de­rives the Lorentz trans­for­ma­tion as dis­cussed in chap­ter 1.2. The ques­tion is what is the re­la­tion­ship be­tween the time and spa­tial co­or­di­nates $t_{\rm {A}},x_{\rm {A}},y_{\rm {A}},z_{\rm {A}}$ that an ob­server A at­taches to an ar­bi­trary event ver­sus the co­or­di­nates $t_{\rm {B}},x_{\rm {B}},y_{\rm {B}},z_{\rm {B}}$ that an ob­server B at­taches to them.

Note that since the choices what to de­fine as time zero and as the ori­gin are quite ar­bi­trary, it can be arranged that $x_{\rm {B}},y_{\rm {B}},z_{\rm {B}},t_{\rm {B}}$ are all zero when $x_{\rm {A}},y_{\rm {A}},z_{\rm {A}},t_{\rm {A}}$ are all zero. That sim­pli­fies the math­e­mat­ics, so it will be as­sumed. It will also be as­sumed that the axis sys­tems of the two ob­servers are taken to be par­al­lel and that the $x$ axes are along the di­rec­tion of rel­a­tive mo­tion be­tween the ob­servers, fig­ure 1.2.

It will fur­ther be as­sumed that the re­la­tion­ship be­tween the co­or­di­nates is lin­ear;

$$\begin{array}{ccc} t_{\rm {B}} = a_{tx} x_{\rm {A}} + a_{... ...\rm {A}} + a_{zz} z_{\rm {A}} + a_{zt} t_{\rm {A}} \end{array}$$

where the $a_{..}$ are con­stants still to be found.

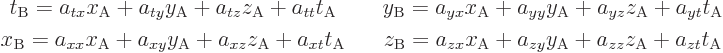
The biggest rea­son to as­sume that the trans­for­ma­tion should be lin­ear is that if space is pop­u­lated with ob­servers A and B, rather than just have a sin­gle one sit­ting at the ori­gin of that co­or­di­nate sys­tem, then a lin­ear trans­for­ma­tion as­sures that all pairs of ob­servers A and B see the ex­act same trans­for­ma­tion. In ad­di­tion, the trans­for­ma­tion from $x_{\rm {B}},y_{\rm {B}},z_{\rm {B}},t_{\rm {B}}$ back to $x_{\rm {A}},y_{\rm {A}},z_{\rm {A}},t_{\rm {A}}$ should be of the same form as the one the other way, since the prin­ci­ple of rel­a­tiv­ity as­serts that the two co­or­di­nate sys­tems are equiv­a­lent. A lin­ear trans­for­ma­tion has a back trans­for­ma­tion that is also lin­ear.

An­other way to look at it is to say that the spa­tial and tem­po­ral scales seen by nor­mal ob­servers are minis­cule com­pared to the scales of the uni­verse. Based on that idea you would ex­pect that the re­la­tion be­tween their co­or­di­nates would be a lin­earized Tay­lor se­ries.

A lot of ad­di­tional con­straints can be put in be­cause of phys­i­cal sym­me­tries that surely still ap­ply even al­low­ing for rel­a­tiv­ity. For ex­am­ple, the trans­for­ma­tion to $x_{\rm {B}},t_{\rm {B}}$ should not de­pend on the ar­bi­trar­ily cho­sen pos­i­tive di­rec­tions of the $y$ and $z$ axes, so throw out the $y$ and $z$ terms in those equa­tions. Seen in a mir­ror along the $xy$-​plane, the $y$ trans­for­ma­tion should look the same, even if $z$ changes sign, so throw out $z_{\rm {A}}$ from the equa­tion for $y_{\rm {B}}$. Sim­i­larly, there goes $y_{\rm {A}}$ in the equa­tion for $z_{\rm {B}}$. Since the choice of $y$ and $z$ axes is ar­bi­trary, the re­main­ing $a_{z.}$ co­ef­fi­cients must equal the cor­re­spond­ing $a_{y.}$ ones. Since the ba­sic premise of rel­a­tiv­ity is that the co­or­di­nate sys­tems A and B are equiv­a­lent, the $y$ dif­fer­ence be­tween tracks par­al­lel to the di­rec­tion of mo­tion can­not get longer for B and shorter for A, nor vice-versa, so $a_{yy}$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1. Fi­nally, by the very de­f­i­n­i­tion of the rel­a­tive ve­loc­ity $v$ of co­or­di­nate sys­tem B with re­spect to sys­tem A, $x_{\rm {B}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $y_{\rm {B}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $z_{\rm {B}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 should cor­re­spond to $x_{\rm {A}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $vt_{\rm {A}}$. And by the prin­ci­ple of rel­a­tiv­ity, $x_{\rm {A}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $y_{\rm {A}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $z_{\rm {A}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 should cor­re­spond to $x_{\rm {B}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $-vt_{\rm {B}}$.

You might be able to think up some more con­straints, but this will do. Put it all to­gether to get

$$\begin{array}{ccc} t_{\rm {B}} = a_{tx} x_{\rm {A}} + a_{x... ...yx} x_{\rm {A}} + z_{\rm {A}} + a_{yt} t_{\rm {A}} \end{array}$$

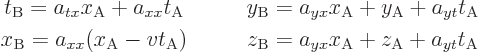
Next the trick is to con­sider the wave front emit­ted by some light source that flashes at time zero at the then co­in­cid­ing ori­gins. Since ac­cord­ing to the prin­ci­ple of rel­a­tiv­ity the two co­or­di­nate sys­tems are fully equiv­a­lent, in both co­or­di­nate sys­tems the wave front forms an ex­pand­ing spher­i­cal shell with ra­dius $ct$:

$$x_{\rm {A}}^2 + y_{\rm {A}}^2 + z_{\rm {A}}^2 = c^2 t_{\rm ... ...\rm {B}}^2 + y_{\rm {B}}^2 + z_{\rm {B}}^2 = c^2 t_{\rm {B}}^2$$

Plug the lin­earized ex­pres­sions for $x_{\rm {B}},y_{\rm {B}},z_{\rm {B}},t_{\rm {B}}$ in terms of $x_{\rm {A}},y_{\rm {A}},z_{\rm {A}},t_{\rm {A}}$ into the sec­ond equa­tion and de­mand that it is con­sis­tent with the first equa­tion, and you ob­tain the Lorentz trans­for­ma­tion. To get the back trans­for­ma­tion giv­ing $x_{\rm {A}},y_{\rm {A}},z_{\rm {A}},t_{\rm {A}}$ in terms of $x_{\rm {B}},y_{\rm {B}},z_{\rm {B}},t_{\rm {B}}$, solve the Lorentz equa­tions for $x_{\rm {A}}$, $y_{\rm {A}}$, $z_{\rm {A}}$, and $t_{\rm {A}}$.

To de­rive the given trans­for­ma­tions be­tween the ve­loc­i­ties seen in the two sys­tems, take dif­fer­en­tials of the Lorentz trans­for­ma­tion for­mu­lae. Then take ra­tios of the cor­re­spond­ing in­fin­i­tes­i­mal po­si­tion in­cre­ments over the cor­re­spond­ing time in­cre­ments.