| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
N.24 A problem if the energy is given
Examining all shelf number combinations with the given energy and then
picking out the combination that has the most energy eigenfunctions
seems straightforward enough, but it runs into a problem. The problem
arises when it is required that the set of shelf numbers agrees with
the given energy to mathematical precision. To see the problem,
recall the simple model system of chapter 11.3 that had only
three energy shelves. Now assume that the energy of the second shelf
is not 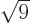
 3 as assumed there, (still arbitrary units),
but slightly less at
3 as assumed there, (still arbitrary units),
but slightly less at 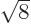 . The difference is small, and
all figures of chapter 11.3 are essentially unchanged.
However, if the average energy per particle is still assumed equal to
2.5, so that the total system energy equals the number of particles
. The difference is small, and
all figures of chapter 11.3 are essentially unchanged.
However, if the average energy per particle is still assumed equal to
2.5, so that the total system energy equals the number of particles
 times that amount, then
times that amount, then  must be zero: it is impossible to
take a nonzero multiple of an irrational number like
must be zero: it is impossible to
take a nonzero multiple of an irrational number like 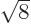 and
end up with a rational number like
and
end up with a rational number like 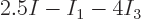 . What this
means graphically is that the oblique energy line in the equivalent of
figure 11.5 does not hit any of the centers of the squares
mathematically exactly, except for the one at
. What this
means graphically is that the oblique energy line in the equivalent of
figure 11.5 does not hit any of the centers of the squares
mathematically exactly, except for the one at 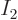
 0. So the
conclusion would be that the system must have zero particles on the
middle shelf.
0. So the
conclusion would be that the system must have zero particles on the
middle shelf.
Of course, physically this is absolute nonsense; the energy of a
large number of perturbed particles is not going to be certain to be
2.5  to mathematical precision. There will be some
uncertainty in energy, and the correct shelf numbers are still those
of the darkest square, even if its energy is 2.499 9...
to mathematical precision. There will be some
uncertainty in energy, and the correct shelf numbers are still those
of the darkest square, even if its energy is 2.499 9... instead of 2.5
instead of 2.5  exactly. Here typical textbooks will pontificate
about the accuracy of your system-energy measurement device. However,
this book shudders to contemplate what happens physically in your
glass of ice water if you have three system-energy measurement
devices, but your best one is in the shop, and you are uncertain
whether to believe the unit you got for cheap at Wal-Mart or your
backup unit with the sticking needle.
exactly. Here typical textbooks will pontificate
about the accuracy of your system-energy measurement device. However,
this book shudders to contemplate what happens physically in your
glass of ice water if you have three system-energy measurement
devices, but your best one is in the shop, and you are uncertain
whether to believe the unit you got for cheap at Wal-Mart or your
backup unit with the sticking needle.
To avoid these conundrums, in this book it will simply be assumed that
the right combination of shelf occupation numbers is still the one at
the maximum in figure 11.6, i.e. the maximum when the
number of energy eigenfunctions is mathematically interpolated by a
continuous function. Sure, that may mean that the occupation numbers
are no longer exact integers. But who is going to count 10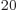 particles to check that it is exactly right? (And note that those
other books end up doing the same thing anyway in the end, since the
mathematics of an integer-valued function defined on a strip is so
much more impossible than that of a continuous function defined on a
line.)
particles to check that it is exactly right? (And note that those
other books end up doing the same thing anyway in the end, since the
mathematics of an integer-valued function defined on a strip is so
much more impossible than that of a continuous function defined on a
line.)
If fractional particles bothers you, even among 10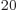 of them,
just fix things after the fact. After finding the fractional shelf
numbers that have the biggest energy, select the whole shelf numbers
nearest to it and then change the
of them,
just fix things after the fact. After finding the fractional shelf
numbers that have the biggest energy, select the whole shelf numbers
nearest to it and then change the given
energy to be
2.499 999 9...or whatever it turns out to be at those whole
shelf numbers. Then you should have perfectly correct shelf numbers
with the highest number of eigenfunctions for the new given energy.
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()