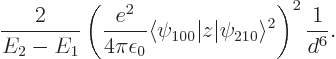| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.33 Explanation of the London forces
To fully understand the details of the London forces, it helps to
first understand the popular explanation of them, and why it is all
wrong. To keep things simple, the example will be the London
attraction between two neutral hydrogen atoms that are well apart.
(This will also correct a small error that the earlier discussion of
the hydrogen molecule made; that discussion implied incorrectly that
there is no attraction between two neutral hydrogen atoms that are far
apart. The truth is that there really is some Van der Waals
attraction. It was ignored because it is small compared to the
chemical bond that forms when the atoms are closer together and would
distract from the real story.)
Figure A.23:
Possible polarizations of a pair of hydrogen atoms.
![\begin{figure}\centering
{}%
\setlength{\unitlength}{1pt}
\begin{picture}(3...
...{\it c})}}
\put(10,68){\makebox(0,0)[tl]{{\it d})}}
\end{picture}
\end{figure}](img5191.gif) |
The popular explanation for the London force goes something like this:
“Sure, there would not be any attraction between two distant
hydrogen atoms if they were perfectly spherically symmetric. But
according to quantum mechanics, nature is uncertain. So sometimes the
electron clouds of the two atoms are somewhat to the left of the
nuclei, like in figure A.23 (b). This
polarization [dipole creation] of the atoms turns out to produce some
electrostatic attraction between the atoms. At other times, the
electron clouds are somewhat to the right of the nuclei like in figure
A.23 (c); it is really the same thing seen in the
mirror. In cases like figure A.23 (a), where the
electron clouds move towards each other, and (b), where they
move away from each other, there is some repulsion between the atoms;
however, the wave functions become correlated so that (b) and
(c) are more likely than (a) and (d). Hence a
net attraction results.”
Before examining what is wrong with this explanation, first consider
what is right. It is perfectly right that figure A.23
(b) and (c) produce some net attraction between the
atoms, and that (a) and (d) produce some repulsion.
This follows from the net Coulomb potential energy between the atoms
for given positions of the electrons:
where 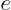
 1.6 10
1.6 10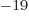 C is the magnitude of the charges of the
protons and electrons,
C is the magnitude of the charges of the
protons and electrons, 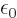
 8.85 10
8.85 10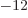 C
C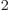 /J m is
the permittivity of space,
/J m is
the permittivity of space, 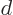 is the distance between the nuclei,
is the distance between the nuclei,
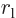 is the distance between the left electron and the right
nucleus,
is the distance between the left electron and the right
nucleus, 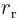 the one between the right electron and the left
nucleus, and
the one between the right electron and the left
nucleus, and 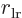 is the distance between the two electrons.
If the electrons charges are distributed over space according to
densities
is the distance between the two electrons.
If the electrons charges are distributed over space according to
densities 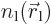 and
and 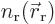 ,
the classical potential energy is
,
the classical potential energy is
(Since the first, 1/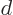 , term represents the repulsion between
the nuclei, it may seem strange to integrate it against the
electron charge distributions, but the charge distributions
integrate to one, so they disappear. Similarly in the second and
third term, the charge distribution of the uninvolved electron
integrates away.)
, term represents the repulsion between
the nuclei, it may seem strange to integrate it against the
electron charge distributions, but the charge distributions
integrate to one, so they disappear. Similarly in the second and
third term, the charge distribution of the uninvolved electron
integrates away.)
Since it is assumed that the atoms are well apart, the integrand above
can be simplified using Taylor series expansions to give:
where the positions of the electrons are measured from their
respective nuclei. Also, the two  axes are both taken horizontal
and positive towards the left. For charge distributions as shown in
figure A.23, the
axes are both taken horizontal
and positive towards the left. For charge distributions as shown in
figure A.23, the 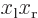 and
and
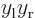 terms integrate to zero because of odd
symmetry. However, for a distribution like in figure
A.23 (c),
terms integrate to zero because of odd
symmetry. However, for a distribution like in figure
A.23 (c), 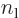 and
and 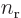 are larger
at positive
are larger
at positive 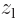 , respectively
, respectively 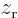 , than
at negative one, so the integral will integrate to a negative number.
That means that the potential is lowered, there is attraction between
the atoms. In a similar way, distribution (b) produces
attraction, while (a) and (d) produce repulsion.
, than
at negative one, so the integral will integrate to a negative number.
That means that the potential is lowered, there is attraction between
the atoms. In a similar way, distribution (b) produces
attraction, while (a) and (d) produce repulsion.
So there is nothing wrong with the claim that (b) and
(c) produce attraction, while (a) and (d)
produce repulsion. It is also perfectly right that the combined
quantum wave function gives a higher probability to (b) and
(c) than to (a) and (d).
So what is wrong? There are two major problems with the story.
-
1.
- Energy eigenstates are stationary. If the wave function
oscillated in time like the story suggests, it would require
uncertainty in energy, which would act to kill off the lowering of
energy. True, states with the electrons at the same side of their
nuclei are more likely to show up when you measure them, but to reap
the benefits of this increased probability, you must not do
such a measurement and just let the electron wave function sit there
unchanging in time.
-
2.
- The numbers are all wrong. Suppose the wave functions in
figures (b) and (c) shift (polarize) by a typical
small amount
 . Then the attractive potential is
of order
. Then the attractive potential is
of order 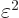

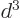 . Since the distance
. Since the distance 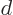 between the atoms is assumed large, the energy gained is a small
amount times
between the atoms is assumed large, the energy gained is a small
amount times 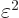 . But to shift atom energy
eigenfunctions by an amount
. But to shift atom energy
eigenfunctions by an amount  away from their ground
state takes an amount of energy
away from their ground
state takes an amount of energy 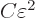 where
where 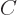 is some
constant that is not small. So it would take more energy to
shift the electron clouds than the dipole attraction could recover.
In the ground state, the electron clouds should therefore stick to
their original centered positions.
is some
constant that is not small. So it would take more energy to
shift the electron clouds than the dipole attraction could recover.
In the ground state, the electron clouds should therefore stick to
their original centered positions.
On to the correct quantum explanation. First the wave function is
needed. If there were no Coulomb potentials linking the atoms, the
combined ground-state electron wave function would simply take the
form
where 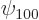 is the ground state wave function of a single
hydrogen atom. To get a suitable correlated polarization of the
atoms, throw in a bit of the
is the ground state wave function of a single
hydrogen atom. To get a suitable correlated polarization of the
atoms, throw in a bit of the 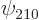
2p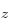
states, as follows:
For 
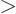 0, it produces the desired correlation between the
wave functions:
0, it produces the desired correlation between the
wave functions: 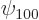 is always positive, and
is always positive, and 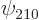 is
positive if the electron is at the positive-
is
positive if the electron is at the positive- side of its nucleus
and negative otherwise. So if both electrons are at the same side of
their nucleus, the product
side of its nucleus
and negative otherwise. So if both electrons are at the same side of
their nucleus, the product
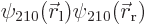 is positive, and
the wave function is increased, giving increased probability of such
states. Conversely, if the electrons are at opposite sides of their
nucleus,
is positive, and
the wave function is increased, giving increased probability of such
states. Conversely, if the electrons are at opposite sides of their
nucleus, 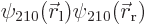 is
negative, and the wave function is reduced.
is
negative, and the wave function is reduced.
Now write the expectation value of the energy:
where 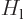 and
and 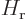 are the Hamiltonians of the
individual electrons and
are the Hamiltonians of the
individual electrons and
is again the potential between atoms. Working out the inner product,
noting that the 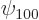 and
and 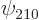 are orthonormal
eigenfunctions of the atom Hamiltonians
are orthonormal
eigenfunctions of the atom Hamiltonians 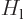 and
and 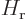 with eigenvalues
with eigenvalues 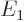 and
and 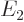 , and that most
, and that most 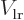 integrals are zero on account of odd symmetry, you get
integrals are zero on account of odd symmetry, you get
The final term is the savior for deriving the London force. For small
values of  , for which the square root can be
approximated as one, this energy-lowering term dominates the energy
, for which the square root can be
approximated as one, this energy-lowering term dominates the energy
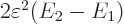 needed to distort the atom wave functions.
The best approximation to the true ground state is then obtained when
the quadratic in
needed to distort the atom wave functions.
The best approximation to the true ground state is then obtained when
the quadratic in  is minimal. That happens when the
energy has been lowered by an amount
is minimal. That happens when the
energy has been lowered by an amount
Since the assumed eigenfunction is not exact, this variational
approximation will underestimate the actual London force. For
example, it can be seen that the energy can also be lowered similar
amounts by adding some of the 2p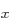 and 2p
and 2p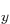 states;
these cause the atom wave functions to move in opposite directions
normal to the line between the nuclei.
states;
these cause the atom wave functions to move in opposite directions
normal to the line between the nuclei.
So what is the physical meaning of the savior term? Consider the
inner product that it represents:
That is the energy if both electrons are in the spherically symmetric
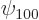 ground state if both electrons are in the antisymmetric
2p
ground state if both electrons are in the antisymmetric
2p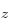 state. The savior term is a twilight term, like the
ones discussed earlier in chapter 5.3 for chemical bonds.
It reflects nature’s habit of doing business in terms of an
unobservable wave function instead of observable probabilities.
state. The savior term is a twilight term, like the
ones discussed earlier in chapter 5.3 for chemical bonds.
It reflects nature’s habit of doing business in terms of an
unobservable wave function instead of observable probabilities.
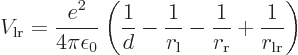
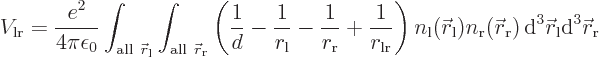
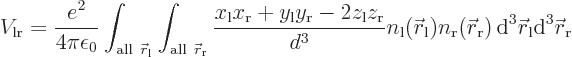
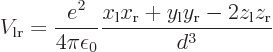
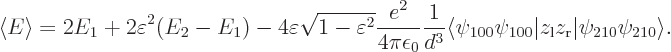
![]() ,
,![]()
![]()