|
|
|
|
|
Next: A.8 Positive ground state wave function |
|
This note has a closer look at the accuracy of the variational method.
Any approximate ground state wave function ![]()
![]() ,
,![]() ,
,
The wave function pollution with higher energy states can be related
to the error in energy, call it ![]() ,
,![]()
![]()
![]()
Note first that since all the terms in the right hand side are
positive, any approximate wave function has more expectation energy
than the ground state ![]() .
.
Nor is it surprising that the expression above shows that the error in
energy ![]()
![]()
![]()
However, note that while the errors in wave function are directly
proportional to the coefficients ![]() ,
,small
is defined in a meaningful nondimensional way.)
That small error in energy is great because the computed energy is important for a number of things, like determining whether a stable ground state of the supposed form exists in the first place, and if it does, how fast it interacts with other energy eigenfunctions if there is uncertainty in energy, chapter 7.
While it may seem obvious that if the approximate wave function is close to the correct one, then the approximate energy will be close to the correct one, the reverse is less trivial. If the approximate energy is close to the exact energy, does that necessarily mean that entire wave function is close to the exact one? Fortunately, the answer to that question is usually yes.
In particular, note from the expression for the error in energy above
that for any coefficient ![]()
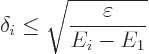
But do also note the effect of the denominator. If it too is small, it
may increase the possible error. The worst case occurs for the second
lowest energy state. If the second-lowest energy ![]()
![]() ,
,![]()
Consider also the magnitude of the error in the approximate wave
function. It is defined as
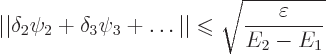
The bottom line is that the lower you can get your expectation energy, the closer you will get to the true ground state energy. In addition the small error in energy will reflect in a small error in wave function too.