| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.17 Inner product for the expectation value
To see that 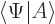 works for getting the expectation value,
just write
works for getting the expectation value,
just write 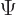 out in terms of the eigenfunctions
out in terms of the eigenfunctions 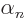 of
of
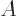 :
:
Now by the definition of eigenfunctions 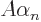

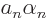 for every
for every 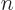 , so you get
, so you get
Since eigenfunctions are orthonormal:
So, multiplying out produces the desired result:
![]()
![]()
![]()
![]() :
: