| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.42 Derivation of the Einstein A coefficients
Einstein did not really derive the spontaneous emission rate from
relativistic quantum mechanics. That did not exist at the time.
Instead Einstein used a dirty trick; he peeked at the solution.
To see how, consider a system of identical atoms that can be in a low
energy state 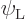 or in an excited energy state
or in an excited energy state
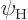 . The fraction of atoms in the low energy state
is
. The fraction of atoms in the low energy state
is 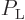 and the fraction in the excited energy state is
and the fraction in the excited energy state is
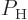 . Einstein assumed that the fraction
. Einstein assumed that the fraction 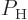 of excited atoms would evolve according to the equation
of excited atoms would evolve according to the equation
where 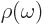 is the ambient electromagnetic field energy
density,
is the ambient electromagnetic field energy
density, 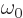 the frequency of the photon emitted in a
transition from the high to the low energy state, and the
the frequency of the photon emitted in a
transition from the high to the low energy state, and the  and
and 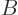 values are constants. This assumption agrees with the expression
(7.46) given in chapter 7.8.
values are constants. This assumption agrees with the expression
(7.46) given in chapter 7.8.
Then Einstein demanded that in an equilibrium situation, in which
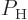 is independent of time, the formula must agree with
Planck’s formula for the blackbody electromagnetic radiation
energy. The equilibrium version of the formula above gives the energy
density as
is independent of time, the formula must agree with
Planck’s formula for the blackbody electromagnetic radiation
energy. The equilibrium version of the formula above gives the energy
density as
Equating this to Planck’s blackbody spectrum as derived in chapter
6.8 (6.11) gives
The atoms can be modeled as distinguishable particles. Therefore the
ratio 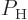

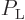 can be found from the
Maxwell-Boltzmann formula of chapter 6.14; that gives the
ratio as
can be found from the
Maxwell-Boltzmann formula of chapter 6.14; that gives the
ratio as 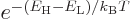 , or
, or
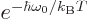 in terms of the photon frequency. It then
follows that for the two expressions for
in terms of the photon frequency. It then
follows that for the two expressions for 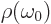 to be equal,
to be equal,
That 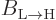 must equal
must equal 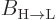 is a consequence
of the symmetry property mentioned at the end of chapter
7.7.2. But it was not self-evident when Einstein wrote the
paper; Einstein really invented stimulated emission here.
is a consequence
of the symmetry property mentioned at the end of chapter
7.7.2. But it was not self-evident when Einstein wrote the
paper; Einstein really invented stimulated emission here.
The valuable result for this book is the formula for the spontaneous
emission rate 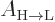 . With
. With 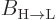 given
by (7.47), it determines the spontaneous emission rate. So
it has been obtained without using relativistic quantum mechanics.
(Or at least not explicitly; there simply are no nonrelativistic
photons.)
given
by (7.47), it determines the spontaneous emission rate. So
it has been obtained without using relativistic quantum mechanics.
(Or at least not explicitly; there simply are no nonrelativistic
photons.)
![]()
![]() .
.![]()
![]() .
.![]()
![]()
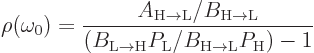
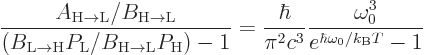
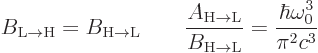
![]()
![]()
![]() .
.![]()