| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.34 The adiabatic theorem
Consider the Schrödinger equation
If the Hamiltonian is independent of time, the solution can be written
in terms of the Hamiltonian energy eigenvalues 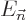 and
eigenfunctions
and
eigenfunctions 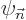 as
as
Here 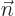 stands for the quantum numbers of the eigenfunctions and
the
stands for the quantum numbers of the eigenfunctions and
the 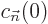 are arbitrary constants.
are arbitrary constants.
However, the Hamiltonian varies with time for the systems of interest
here. Still, at any given time its eigenfunctions form a complete
set. So it is still possible to write the wave function as a sum of
them, say like
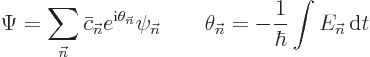 |
(D.18) |
But the coefficients 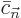 can no longer be assumed to be
constant like the
can no longer be assumed to be
constant like the 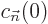 . They may be different at
different times.
. They may be different at
different times.
To get an equation for their variation, plug the expression for 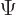 in the Schrödinger equation. That gives:
in the Schrödinger equation. That gives:
where the primes indicate time derivatives. The middle sum in the
left hand side and the right hand side cancel against each other since
by definition 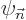 is an eigenfunction of the Hamiltonian with
eigenvalue
is an eigenfunction of the Hamiltonian with
eigenvalue 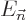 . For the remaining two sums, take an inner
product with an arbitrary eigenfunction
. For the remaining two sums, take an inner
product with an arbitrary eigenfunction 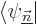 :
:
In the first sum only the term 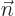

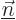 survived because of the
orthonormality of the eigenfunctions. Divide by
survived because of the
orthonormality of the eigenfunctions. Divide by
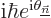 and rearrange to get
and rearrange to get
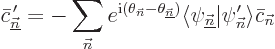 |
(D.19) |
This is still exact.
However, the purpose of the current derivation is to address the
adiabatic approximation. The adiabatic approximation assumes that the
entire evolution takes place very slowly over a large time interval
 . For such an evolution, it helps to consider all quantities
to be functions of the scaled time variable
. For such an evolution, it helps to consider all quantities
to be functions of the scaled time variable 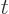

 . Variables
change by a finite amount when
. Variables
change by a finite amount when 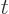 changes by a finite fraction of
changes by a finite fraction of
 , so when
, so when 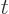

 changes by a finite amount. This implies
that the time derivatives of the slowly varying quantities are
normally small, of order 1/
changes by a finite amount. This implies
that the time derivatives of the slowly varying quantities are
normally small, of order 1/ .
.
Consider now first the case that there is no degeneracy, in other
words, that there is only one eigenfunction 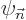 for each energy
for each energy
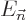 . If the Hamiltonian changes slowly and regularly in
time, then so do the energy eigenvalues and eigenfunctions. In
particular, the time derivatives of the eigenfunctions in
(D.19) are small of order 1/
. If the Hamiltonian changes slowly and regularly in
time, then so do the energy eigenvalues and eigenfunctions. In
particular, the time derivatives of the eigenfunctions in
(D.19) are small of order 1/ . It then follows from
the entire equation that the time derivatives of the coefficients are
small of order 1
. It then follows from
the entire equation that the time derivatives of the coefficients are
small of order 1
 too.
too.
(Recall that the square magnitudes of the coefficients give the
probability for the corresponding energy. So the magnitude of the
coefficients is bounded by 1. Also, for simplicity it will be assumed
that the number of eigenfunctions in the system is finite. Otherwise
the sums over 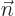 might explode. This book routinely assumes that
it is
might explode. This book routinely assumes that
it is good enough
to approximate an infinite system by
a large-enough finite one. That makes life a lot easier, not just
here but also in other derivations like {D.18}.)
It is convenient to split up the sum in (D.19):
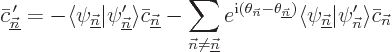 |
(D.20) |
Under the stated conditions, the final sum can be ignored.
However, that is not because it is small due to the time derivative in
it, as one reference claims. While the time derivative of 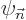 is indeed small of order 1/
is indeed small of order 1/ , it acts over a time that is
large of order
, it acts over a time that is
large of order  . The sum can be ignored because of the
exponential in it. As the definition of
. The sum can be ignored because of the
exponential in it. As the definition of 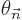 shows, it varies
on the normal time scale, rather than on the long time scale
shows, it varies
on the normal time scale, rather than on the long time scale
 . Therefore it oscillates many times on the long time scale;
that causes opposite values of the exponential to largely cancel each
other.
. Therefore it oscillates many times on the long time scale;
that causes opposite values of the exponential to largely cancel each
other.
To show that more precisely, note that the formal solution of the full
equation (D.20) is, [41, 19.2]:
 |
(D.21) |
To check this solution, you can just plug it in. Note in doing so
that the integrands are taken to be functions of 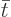 , not
, not
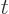 .
.
All the integrals are negligibly small because of the rapid variation
of the first exponential in them. To verify that, rewrite them a bit
and then perform an integration by parts:
The first term in the right hand side is small of order 1
 because
the time derivative of the wave function is. The integrand in the
second term is small of order 1
because
the time derivative of the wave function is. The integrand in the
second term is small of order 1
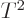 because of the two time
derivatives. So integrated over an order
because of the two time
derivatives. So integrated over an order  time range, it is small
of order 1
time range, it is small
of order 1
 like the first term. It follows that the integrals in
(D.21) become zero in the limit
like the first term. It follows that the integrals in
(D.21) become zero in the limit  .
.
And that means that in the adiabatic approximation
The underbar used to keep 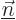 and
and 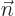 apart is no longer needed
here since only one set of quantum numbers appears. This expression
for the coefficients can be plugged in (D.18) to find the
wave function
apart is no longer needed
here since only one set of quantum numbers appears. This expression
for the coefficients can be plugged in (D.18) to find the
wave function 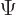 . The constants
. The constants 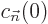 depend on the
initial condition for
depend on the
initial condition for 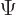 . (They also depend on the choice of
integration constants for
. (They also depend on the choice of
integration constants for 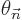 and
and 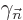 , but
normally you take the phases zero at the initial time).
, but
normally you take the phases zero at the initial time).
Note that 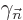 is real. To verify that, differentiate the
normalization requirement to get
is real. To verify that, differentiate the
normalization requirement to get
So the sum of the inner product plus its complex conjugate are zero.
That makes it purely imaginary, so 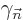 is real.
is real.
Since both 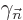 and
and 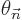 are real, it follows that
the magnitudes of the coefficients of the eigenfunctions do not change
in time. In particular, if the system starts out in a single
eigenfunction, then it stays in that eigenfunction.
are real, it follows that
the magnitudes of the coefficients of the eigenfunctions do not change
in time. In particular, if the system starts out in a single
eigenfunction, then it stays in that eigenfunction.
So far it has been assumed that there is no degeneracy, at least not
for the considered state. However it is no problem if at a finite
number of times, the energy of the considered state crosses some other
energy. For example, consider a three-dimensional harmonic oscillator
with three time varying spring stiffnesses. Whenever any two
stiffnesses become equal, there is significant degeneracy. Despite
that, the given adiabatic solution still applies. (This does assume
that you have chosen the eigenfunctions to change smoothly through
degeneracy, as perturbation theory says you can, {D.79}.)
To verify that the solution is indeed still valid, cut out a time
interval of size 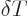 around each crossing time. Here
around each crossing time. Here  is some number still to be chosen. The parts of the integrals in
(D.21) outside of these intervals have magnitudes
is some number still to be chosen. The parts of the integrals in
(D.21) outside of these intervals have magnitudes
 that become zero when
that become zero when  for the
same reasons as before. The parts of the integrals corresponding to
the intervals can be estimated as no more than some finite multiple of
for the
same reasons as before. The parts of the integrals corresponding to
the intervals can be estimated as no more than some finite multiple of
 . The reason is that the integrands are of order 1
. The reason is that the integrands are of order 1
 and they are integrated over ranges of size
and they are integrated over ranges of size 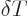 . All
together, that is enough to show that the complete integrals are less
than say 1%; just take
. All
together, that is enough to show that the complete integrals are less
than say 1%; just take  small enough that the intervals
contribute no more than 0.5% and then take
small enough that the intervals
contribute no more than 0.5% and then take  large enough that the
remaining integration range contributes no more than 0.5% too. Since
you can play the same game for 0.1%, 0.01% or any arbitrarily small
amount, the conclusion is that for infinite
large enough that the
remaining integration range contributes no more than 0.5% too. Since
you can play the same game for 0.1%, 0.01% or any arbitrarily small
amount, the conclusion is that for infinite  , the
contribution of the integrals becomes zero. So in the limit
, the
contribution of the integrals becomes zero. So in the limit
 , the adiabatic solution applies.
, the adiabatic solution applies.
Things change if some energy levels are permanently degenerate.
Consider an harmonic oscillator for which at least two spring
stiffnesses are permanently equal. In that case, you need to solve
for all coefficients at a given energy level 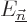 together. To
figure out how to do that, you will need to consult a book on
mathematics that covers systems of ordinary differential equations.
In particular, the coefficient
together. To
figure out how to do that, you will need to consult a book on
mathematics that covers systems of ordinary differential equations.
In particular, the coefficient 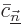 in (D.21)
gets replaced by a vector of coefficients with the same energy. The
scalar
in (D.21)
gets replaced by a vector of coefficients with the same energy. The
scalar 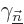 becomes a matrix with indices ranging over the
set of coefficients in the vector. Also,
becomes a matrix with indices ranging over the
set of coefficients in the vector. Also, 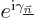 gets
replaced by a
gets
replaced by a fundamental solution matrix,
a matrix
consisting of independent solution vectors. And
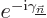 is the inverse matrix. The sum no longer
includes any of the coefficients of the considered energy.
is the inverse matrix. The sum no longer
includes any of the coefficients of the considered energy.
More recent derivations allow the spectrum to be continuous, in which
case the nonzero energy gaps 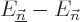 can no longer be assumed
to be larger than some nonzero amount. And unfortunately, assuming
the system to be approximated by a finite one helps only partially
here; an accurate approximation will produce very closely spaced
energies. Such problems are well outside the scope of this book.
can no longer be assumed
to be larger than some nonzero amount. And unfortunately, assuming
the system to be approximated by a finite one helps only partially
here; an accurate approximation will produce very closely spaced
energies. Such problems are well outside the scope of this book.

![]()
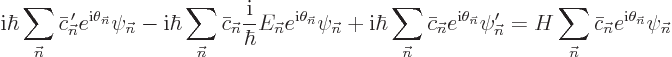
![]() .
.![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![]()
![]() .
.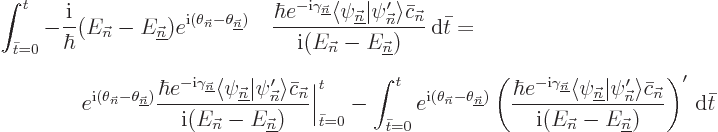
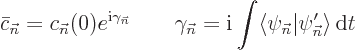
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()