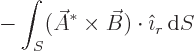| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.10 The curl is Hermitian
For later reference, it will be shown that the curl operator,
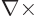 is Hermitian. In other words,
is Hermitian. In other words,
The rules of engagement are as follows:
- The Cartesian axes are numbered using an index
 , with
, with

 1, 2, and 3 for
1, 2, and 3 for  ,
,  , and
, and  respectively.
respectively.
- Also,
 indicates the coordinate in the
indicates the coordinate in the  direction,
direction,
 ,
,  , or
, or  .
.
- Derivatives with respect to a coordinate
 are indicated by
a simple subscript
are indicated by
a simple subscript  .
.
- If the quantity being differentiated is a vector, a comma is
used to separate the vector index from differentiation ones.
- Index
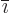 is the number immediately following
is the number immediately following  in the
cyclic sequence ...123123...and
in the
cyclic sequence ...123123...and 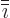 is the number
immediately preceding
is the number
immediately preceding  .
.
- A bare
 integral sign is assumed to be an integration over
all space, or over the entire box for particles in a box. The
integral sign is assumed to be an integration over
all space, or over the entire box for particles in a box. The
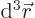 is normally omitted for brevity and to be understood.
is normally omitted for brevity and to be understood.
- A superscript
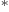 indicates a complex conjugate.
indicates a complex conjugate.
In index notation, the integral in the left hand side above reads:
which is the same as
as can be checked by differentiating out the first two terms. Now the
third and fourth terms in the integral are 
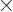
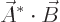 , as you can see from moving all indices in
the third term one unit forward in the cyclic sequence, and those in
the fourth term one unit back. (Such a shift does not change the sum;
the same terms are simply added in a different order.)
, as you can see from moving all indices in
the third term one unit forward in the cyclic sequence, and those in
the fourth term one unit back. (Such a shift does not change the sum;
the same terms are simply added in a different order.)
So, if the integral of the first two terms is zero, the fact that curl
is Hermitian has been verified. Note that the terms can be
integrated. Then, if the system is in a periodic box, the integral is
indeed zero because the upper and lower limits of integration are
equal. An infinite domain will need to be truncated at some large
distance 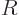 from the origin. Then shift indices and apply the
divergence theorem to get
from the origin. Then shift indices and apply the
divergence theorem to get
where 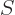 is the surface of the sphere
is the surface of the sphere 

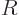 and
and  the unit
vector normal to the sphere surface. It follows that the integral is
zero if
the unit
vector normal to the sphere surface. It follows that the integral is
zero if 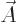 and
and 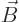 go to zero at infinity quickly enough.
Or at least their cross product has to go to zero quickly enough.
go to zero at infinity quickly enough.
Or at least their cross product has to go to zero quickly enough.
![]()
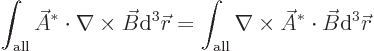
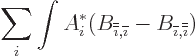
![\begin{displaymath}
\sum_i \int [ (A_i^* B_{\overline{\overline{\imath}}})_{\ov...
... A_{i,{\overline{\overline{\imath}}}}^* B_{\overline{\imath}}]
\end{displaymath}](img5975.gif)
![]()