|
|
|
|
|
Next: 5.2 The Hydrogen Molecule |
|
While a single particle is described by a wave function
![]() ,
,
| (5.1) |
The wave function must be normalized to express that the electrons must be
somewhere:
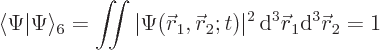 |
(5.2) |
The underlying idea of increasing system size is “every possible combination:” allow for every possible
combination of state for particle 1 and state for particle 2. For
example, in one dimension, all possible ![]()
![]() -
-![]()
![]() -
-![]()
![]() ,
,![]() -
-
Similarly, in three dimensions the three-dimensional space of
positions ![]()
![]()
![]()
![]() .
.
The increase in the number of dimensions when the system size
increases is a major practical problem for quantum mechanics. For
example, a single arsenic atom has 33 electrons, and each
electron has 3 position coordinates. It follows that the wave
function is a function of 99 scalar variables. (Not even counting the
nucleus, spin, etcetera.) In a brute-force numerical solution of the
wave function, maybe you could restrict each position coordinate to
only ten computational values, if no very high accuracy is desired.
Even then, ![]()
![]()
![]()
![]()
Sometimes the problem size can be reduced. In particular, the problem for a two-particle system like the proton-electron hydrogen atom can be reduced to that of a single particle using the concept of reduced mass. That is shown in addendum {A.5}.
Key Points
- To describe multiple-particle systems, just keep adding more independent variables to the wave function.
- Unfortunately, this makes many-particle problems impossible to solve by brute force.
A simple form that a six-dimensional wave function can take is a product of two three-dimensional ones, as in ![]()
![]()
![]() .
.![]()
![]()
![]() .
.
Show that for a simple product wave function as in the previous question, the relative probabilities of finding particle 1 near a position ![]()
![]()
Note: This is the reason that a simple product wave function is called uncorrelated.
For particles that interact with each other, an uncorrelated wave function is often not a good approximation. For example, two electrons repel each other. All else being the same, the electrons would rather be at positions where the other electron is nowhere close. As a result, it really makes a difference for electron 1 where electron 2 is likely to be and vice-versa. To handle such situations, usually sums of product wave functions are used. However, for some cases, like for the helium atom, a single product wave function is a perfectly acceptable first approximation. Real-life electrons are crowded together around attracting nuclei and learn to live with each other.