| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
3.5.8.2 Solution pipeg-b
Question:
At what ratio of 

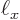 does the energy
does the energy  become higher than the energy
become higher than the energy  ?
?
Answer:
Using the given expression for  ,
,


 when
when
Canceling the terms that both sides have in common:
and canceling the common factors and rearranging:
So when 

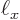


 0.61 or more, the third lowest energy state is given by
0.61 or more, the third lowest energy state is given by  rather than
rather than  . Obviously, it will look more like a box than a pipe then, with the
. Obviously, it will look more like a box than a pipe then, with the  -dimension 61% of the
-dimension 61% of the  -dimension.
-dimension.
![]()
![]()
![]()
![]()
![]() ?
?![]() ,
,


