| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
3.5.8.1 Solution pipeg-a
Question:
If the cross section dimensions  and
and  are one tenth the size of the pipe length, how much bigger are the energies
are one tenth the size of the pipe length, how much bigger are the energies  and
and  compared to
compared to  ? So, by what percentage is the one-dimensional ground state energy
? So, by what percentage is the one-dimensional ground state energy  as an approximation to the three-dimensional one,
as an approximation to the three-dimensional one,  , then in error?
, then in error?
Answer:
The energies are
If  and
and  are ten times smaller than
are ten times smaller than 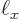 then
then  and
and  are each 100 times larger than
are each 100 times larger than  . So the one-dimensional ground state energy
. So the one-dimensional ground state energy  is smaller than the true ground state energy
is smaller than the true ground state energy 

 by a factor 201. Which means it is off by 20 000%.
by a factor 201. Which means it is off by 20 000%.
![]()
![]()
![]()
![]()
![]() ?
?![]()
![]() ,
,