| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.3.2.3 Solution hydb-c
Question:
Plug numbers into the generic expression for the energy eigenvalues,
where 



 , to find the ground state energy. Express in eV, where 1 eV equals 1.602 2 10
, to find the ground state energy. Express in eV, where 1 eV equals 1.602 2 10 J. Values for the physical constants can be found at the start of this section and in the notations section.
J. Values for the physical constants can be found at the start of this section and in the notations section.
Answer:
First verify the Bohr radius
Next, taking 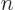
 1 for the ground state,
1 for the ground state,
which gives 

 13.61 eV
13.61 eV


