| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.3.2.2 Solution hydb-b
Question:
Use the generic expression
with 



 and
and  from the spherical harmonics table to find the ground state wave function
from the spherical harmonics table to find the ground state wave function  . Note: the Laguerre polynomial
. Note: the Laguerre polynomial 

 and for any
and for any  ,
,  is just its
is just its  -th derivative.
-th derivative.
Answer:
You get, substituting 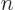
 1,
1, 
 0,
0, 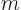
 0:
0:
where 0! = 1! = 1,  is the first derivative of
is the first derivative of 

 with respect to
with respect to  , which is
, which is  1, and
1, and 
 1
1
 according to the table. So you get
according to the table. So you get
as in the previous question.

![]()
![]()
![]()
![]()
![]()
![]()
![\begin{displaymath}
\psi_{100} = -\frac{2}{1^2} \sqrt{\frac{0!}{[1!a_0]^3}} \lef...
...1^1\left(\frac{2\rho}1\right) e^{-\rho /1} Y_0^0(\theta ,\phi)
\end{displaymath}](img341.gif)
