|
|
|
To: Bibliography |
This appendix gives some derivations mentioned earlier
in the various chapters.
First is the derivation of the redistribution
equations (4.8) and following.
We write the difference between the Fourier transform
of the redistributed vorticity (4.5) and the exactly diffused
vorticity (4.6) in terms of
the viscous scale
![]() and
the scaled relative positions (4.7):
and
the scaled relative positions (4.7):
The remaining error in the Fourier transform,
needed in chapter 5,
is according to the Taylor series remainder theorem
To find the lower bound to the redistribution radius mentioned in section
6.2.3, we integrate (A.2) over the unit
circle to produce
 |
(A.6) |
Up to fourth-order accuracy, this estimate for the minimum radius is precise.
It may be verified by direct substitution into
the redistribution equations that
a positive second-order solution is obtained by
spreading the fractions evenly over the circle with scaled radius ![]() .
Similarly, a positive fourth-order solution is obtained by giving the
vortex being redistributed a fraction
.
Similarly, a positive fourth-order solution is obtained by giving the
vortex being redistributed a fraction ![]() and spreading the other half
evenly over the circle
and spreading the other half
evenly over the circle ![]() .
.
Next we verify an assertion made in section 6.2.3:
as long as all vortices are redistributed, the region
containing the vortices must expand a finite scaled amount
in each direction.
To do so, we
derive a lower bound
![]() to
to
![]() using the cases
using the cases
![]() and
and ![]() , 1, and 2 of (A.3):
, 1, and 2 of (A.3):
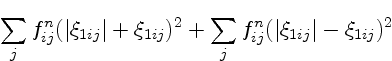 | |||||
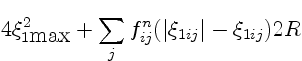 | |||||
 | |||||
| (A.7) |
Next we verify an assertion made in section 6.2.3
and subsection 9.5:
for third-order accuracy or higher, the scaled spacing between the
vortices cannot be arbitrarily large. Defining
![]() and using
(A.5) for
and using
(A.5) for ![]() and
and ![]() , it is seen that
, it is seen that
| (A.9) |
Finally we verify an assertion made in section 6.2.3:
there are finite values ![]() and
and ![]() so that a positive solution
to the redistribution equations exists within the circle with
scaled radius
so that a positive solution
to the redistribution equations exists within the circle with
scaled radius ![]() provided that
there are no square holes exceeding a scaled size
provided that
there are no square holes exceeding a scaled size ![]() in the distribution of the vortices.
To do so, we first note that the diffusing delta function
in the distribution of the vortices.
To do so, we first note that the diffusing delta function
| (A.10) |
| (A.12) |
At least for the case of first-order accuracy, ![]() , for any
, for any
![]() greater than the minimum value
greater than the minimum value ![]() , a finite hole size
, a finite hole size ![]() exists that
ensures a positive solution.
This can be seen by selecting nine vortices to satisfy the redistribution
equations. Eight of these are chosen as closely as possible
to eight equally spaced points on the outside circle
and given a nominal fraction
exists that
ensures a positive solution.
This can be seen by selecting nine vortices to satisfy the redistribution
equations. Eight of these are chosen as closely as possible
to eight equally spaced points on the outside circle
and given a nominal fraction
![]() , and the last point is
chosen to be the vortex being redistributed, and given
a nominal weight
, and the last point is
chosen to be the vortex being redistributed, and given
a nominal weight ![]() .
This satisfies the redistribution equations approximately, and
it is readily seen that for these nominal positions, the needed corrections
in the weights to make the approximation exact can be bounded by the errors.
Thus, similar as in the derivation above, the corrections do not change
the sign of the weights when
.
This satisfies the redistribution equations approximately, and
it is readily seen that for these nominal positions, the needed corrections
in the weights to make the approximation exact can be bounded by the errors.
Thus, similar as in the derivation above, the corrections do not change
the sign of the weights when ![]() is small enough.
The actual value of
is small enough.
The actual value of ![]() is unknown, but clearly
is unknown, but clearly ![]() must tend to zero
when
must tend to zero
when ![]() ;
the allowed hole size must be small enough to ensure that there are vortices
outside the circle
;
the allowed hole size must be small enough to ensure that there are vortices
outside the circle ![]() within which no solution exists.
within which no solution exists.