8.2.5 Drag force

In this section we compare our computed drag force on the cylinder to that obtained in the boundary layer computations of Van Dommelen & Shankar (unpublished); to analytical solutions for small times derived by Collins & Dennis [60]; and to other numerical computations [3,40,117,120,133,170,237,249].

The force on the cylinder per unit length, nondimensionalized by $\rho a U_\infty^2/2$ , is most accurately computed using the equation derived by Graham [94],

$\begin{displaymath} C_L\,-\,iC_D\;=\;\frac{d}{dt}\,\sum_{j}\Gamma_j\, \left(z_j\,-\,\frac{1}{z_j^*}\right) \quad \ , \end{displaymath}$

(8.1)

**Figure 8.24:** Impulsively translated cylinder: Drag coefficient at small times for various Reynolds numbers. Long dashed lines are standard boundary layer theory. Solid lines are second-order boundary layer theory. Dot-dashed lines are the small time expansion of Collins & Dennis [60]. Symbols are vorticity redistribution solutions ( $\Delta t=0.01$ ; $\epsilon _\Gamma =10^{-5}$ for = 550, 1000, & 3,000; $\epsilon _\Gamma =10^{-6}$ for = 9,500; $\epsilon _\Gamma =5 \times 10^{-7}$ for = 20,000; and $\epsilon _\Gamma = 10^{-7}$ for = 40,000).
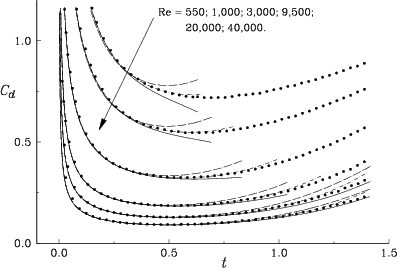$\begin{figure}{\hspace{-1mm} \centerline{\epsfxsize=15.5cm\epsfbox{cd_sm.eps} }}\end{figure}$

Figure 8.24 shows the drag force at early times for Reynolds numbers in the range

according to our numerical results and according to analytical results. The first of the analytical results are the boundary layer computations of Van Dommelen & Shankar (unpublished) that are valid for sufficiently small times or for sufficiently high Reynolds numbers. The broken and solid boundary layer curves in figure 8.24 correspond to different levels of approximation, the solid curve being the more accurate, and we have terminated the curves where significant differences between the two start to show up.

The other analytical results are due to Collins & Dennis [60] and were obtained from expanding the solution analytically in powers of time, leading to ordinary differential equations that are then solved numerically. The expansions were taken as high as sixth order in time and figure 8.24 shows that they remain accurate until quite late. We conjecture that infinite Reynolds number the region of convergence may be as large as up to time

, at which time the exact solution has a singularity (the Van Dommelen & Shen singularity [241]). Note for the highest Reynolds number that near

the results of Collins & Dennis [60] move away from the solid boundary layer curve. Yet, the small difference between the two boundary layer curves, as well as our own data indicate that the solid curve is accurate; it is a higher order approximation than the standard boundary layer curve.

We note that as long as the boundary layer solution is certainly accurate, as indicated by coinciding curves, it also coincides with the results of Collins & Dennis [60] as well as with our numerical data. This is strong support for our results.

All our computations reproduce the singularity in the drag at vanishing time very well. At those early times, half the drag is due to the singular wall shear caused by the vanishingly thin boundary layer while the other half is due to the pressure forces induced by the strong outward diffusion of the boundary layer vorticity, see Van Dommelen & Shankar [229] for a detailed discussion. It is gratifying to see how well our computation reproduces this, even though at the initial time step, our computation approximates the entire boundary layer by a single string of vortices (section 6.3).

Also note that according to the small time expansion, the exact solution is in between the two boundary layer curves when they start to diverge. This agrees well with our computation. It should be expected that the correct solution follows the expansion of Collins & Dennis [60] until their small time assumption breaks down, and our computation does exactly that. Also, note that for higher Reynolds numbers and larger times, when the boundary layer theory is presumably more accurate, our results start following that. Altogether, the analytical solutions provide solid support for the correctness and accuracy of our computation at the times that the analytical data are valid.

**Figure 8.25:** Impulsively translated cylinder, : Drag coefficient. Solid line is our vorticity redistribution solution. Symbols are solutions computed by Koumoutsakos & Leonard [117], Chang & Chern [40], Pépin [170], Van Dommelen [237], and Loc [133].
$\begin{figure}\vspace{7.75in} \centerline{ {\special{psfile=cd5_kl.eps hscale=43... ... hscale=43 vscale=43 hoffset=-240 voffset=15 }} } \vspace{-.8in} \end{figure}$

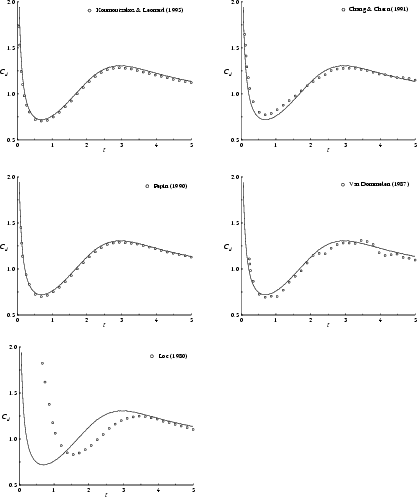
For longer times than can be described by theory, we will compare our computed drag force with other computational results. First, for

, our computed drag is in excellent agreement with that of Koumoutsakos & Leonard [117] and Pépin [170]; see figure 8.25.

**Figure 8.26:** Impulsively translated cylinder, : Drag and lift coefficients. Solid lines are vorticity redistribution solutions ( $\Delta t=0.01$ ; $\epsilon _\Gamma =10^{-6}$ ). The short and long dashed lined are random walk results of Van Dommelen [237] at $\Delta t=0.0125$ and $\Delta t=0.025$ respectively.
$\begin{figure}{\hspace{-8mm} \centerline{\epsfxsize=16.5cm\epsfbox{cdl5_vd.eps} }}\end{figure}$

It is also in fair agreement with the finite difference results of Chang & Chern [40] and with the random walk computation of Van Dommelen [237]. In figure 8.26, we show two different random walk curves obtained by Van Dommelen (different random numbers). The difference between the curves verifies that the errors in the random walk method are responsible for the deviations from our much more accurate results. We do not agree with Loc's [133] results, figure 8.25. Loc's data are also in clear violation of the analytical data of figure 8.24. Further, the close agreement between the best three computations in figure 8.25 provides strong support that our computation remains accurate beyond the times for which the theories apply.

**Figure 8.27:** Impulsively translated cylinder, : Drag coefficient. Solid line is our vorticity redistribution solution. Symbols are solutions computed by Anderson & Reider [3], Koumoutsakos & Leonard [117], Chang & Chern [40], and Pépin [170].
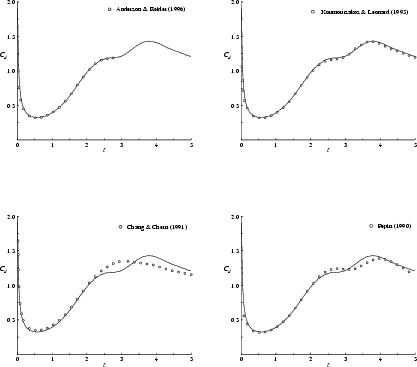$\begin{figure}\vspace{5.5in} \centerline{ {\special{psfile=cd3_ar.eps hscale=43 ... ...ps hscale=43 vscale=43 hoffset=-20 voffset=30 }} } \vspace{-.5in}\end{figure}$

The accuracy of our computed drag is further validated at Reynolds number

in figure 8.27 by the excellent agreement with high resolution computations of Anderson & Reider [3] and Koumoutsakos & Leonard [117].

**Figure 8.28:** Impulsively translated cylinder, , part 1: Drag coefficient. Solid line is our vorticity redistribution solution. Symbols are solutions computed by Anderson & Reider [3], Kruse & Fischer [120], Koumoutsakos & Leonard [117], and Wu, Wu, Ma & Wu [249].
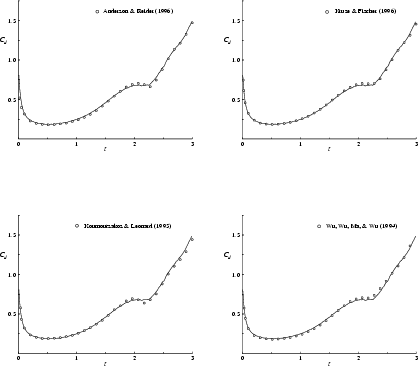
$\begin{figure}\vspace{5.5in} \centerline{ {\special{psfile=cd9_ar.eps hscale=43 ... ...ale=43 vscale=43 hoffset=-20 voffset=30 }} } \par \vspace{-.5in} \end{figure}$

**Figure 8.28:** Impulsively translated cylinder, , part 2: Drag coefficient. Solid line is our vorticity redistribution solution. Symbols are solutions computed by Chang & Chern [40], Pépin [170], and Van Dommelen (unpublished).
$\begin{figure}\vspace{5.5in} \centerline{ {\special{psfile=cd9_cc.eps hscale=43 ... ...3 vscale=43 hoffset=-240 voffset=30 }} } \par \vspace{-.5in}\par \end{figure}$

At Reynolds number

, our results are further validated by excellent agreement with those of Kruse & Fischer [120], Koumoutsakos & Leonard [117], Wu, Wu, Ma & Wu [249] and Anderson & Reider [3]; see figure 8.28. Note however, that there are some minor discrepancies between these computations at the drag ``plateau" near time

. We again tend to believe that our results are the most accurate of all, despite the fact that we use much less computational points as the other computations.

**Figure 8.29:** Impulsively translated cylinder, : Drag coefficient. Long dashed line is $\Delta t=0.04$ . Short dashed line is $\Delta t=0.02$ . Solid line is $\Delta t=0.01$ . For all three cases $\epsilon _\Gamma =10^{-6}$ .
$\begin{figure}{\hspace{10mm} \centerline{\epsfxsize=15.5cm \epsfbox{cd9_dt.eps} }} \end{figure}$

One reason is the apparent computational convergence with numerical resolution shown in figure 8.29. Another reason is that the results of Kruse & Fischer [120], a spectral element computation with over a million nodal points, do not show the ``dip" in the drag experienced by Koumoutsakos & Leonard [117] and Anderson & Reider [3]. See subsections 8.2.6 and 8.2.9 for additional arguments.

**Figure 8.30:** Impulsively translated cylinder, : Drag coefficient. Long dashed line is $\Delta t=0.04$ . Short dashed line is $\Delta t=0.02$ . Solid line is $\Delta t=0.01$ . For all three cases $\epsilon _\Gamma =5 \times 10^{-7}$ .
$\begin{figure}{\hspace{-1mm} \centerline{\epsfxsize=15.5cm\epsfbox{cd2_dt.eps} }} \end{figure}$

In the next section we will explain a difficulty in this type of computations that has not been paid much attention to so far. It may explain some of the difficulties previous computations have experienced.