, of various substances (water, amonia, methane, nitrogen,
refrigerants). The generic problem is: given any two of the intensive
variables of a substance, figure out any other intensive variables you
need.
Revised 5/4/04
The tables in Appendix B of the book1 allow you to
figure out the intensive variables, p, T, v, x (if defined),
, of various substances (water, amonia, methane, nitrogen,
refrigerants). The generic problem is: given any two of the intensive
variables of a substance, figure out any other intensive variables you
need.
Unfortunately, the table to use depends not just on the substance, but also on the phase it is in (when the substance is in vapor form you must a different table than if it is in liquid form, for example.) And to figure out the phase, you need to understand and use either the pv- or the Tv-diagram, as explained in the next section.
The generic shape of a bare Tv-diagram is shown below:
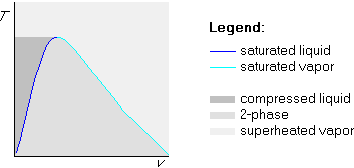
The vertical axis represents the temperature T, while the horizontal axis represents the specific volume v. Each point in the graph represents one particular state of the substance, with the point's height giving the temperature and the point's horizontal position the specific volume.
At the darkest grey points the water is in liquid form; at the lightest grey points the water is in vapor form, and inside the medium grey bell-shaped region the water is a mixture of liquid and vapor.
Points on the dark blue line represents liquid that is just ready to start boiling. Such liquid is called ``saturated liquid.'' The liquid of the darkest grey region is not yet ready to boil; such liquid is more precisely called compressed liquid.
Similarly, on the light blue line, we have vapor that is just ready to start condensing into water; such vapor is called ``saturated vapor.'' The lightest grey points where the vapor is not yet ready to condense into liquid are called ``superheated vapor.''
In the medium gray bell-shaped region, the water is a mixture of saturated liquid and saturated vapor. We will therefor call it the two-phase or saturated region.
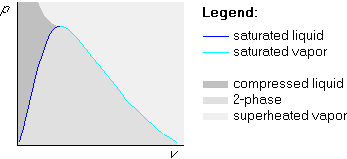
The generic shape of a bare pv-diagram is very similar to that of the bare Tv-diagram in the previous section, but points at the same height now have the same pressure:
An example of an isoline is a horizontal line in a Tv-diagram. Any two points on the same horizontal line in a Tv-diagram have the same temperature. (They will have different pressures, specific volumes, etc, but the temperatures will be the same.) A line on which all states have the same temperature is called an isotherm. So, horizontal lines in the Tv-diagram are isotherms.
On a vertical line in the Tv diagram, (or in the pv diagram for that matter), all points have the same specific volume. Such a line is called an isochore.
The picture below shows examples of isolines in the Tv-diagram. We already mentioned that any horizontal line is an isotherm, on which all points have the same temperature. Similarly, any vertical line is an isochore, on which all points have the same specific volume. New are the isobars, which are lines on which all points have the same pressure. (Recall that a bar is a unit of pressure and a barometer is a device to measure pressure.)
Isobars in the Tv-diagram are not straight: starting from a small specific volume in the compressed liquid region, they first go up. Next they stay horizontal in the two phase region, (like the isotherm in that region), and then they go up again when they cross into the superheated vapor region. It is important to remember this shape:
Isolines in the pv-diagram are quite different. First of all, isobars are now horizontal straight lines, since the vertical coordinate is pressure. Isotherms are no longer straight:
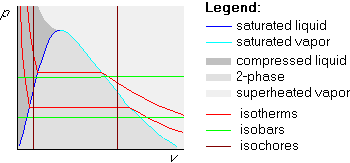
It is easy to remember that isobars are straight horizontal lines and isochores are straight vertical lines, because p and v are on the axes. But remember:
Before trying to figure out example states in the next section, let's have a first look at some typical tables, taking those for water, (``the steam tables''), as an example.
Table B.1.1 gives the properties of the saturated lines. Those are the dark and light blue lines in the Tv and pv-diagrams. Saturated tables are one dimensional: you need only a single number to figure out your place in the table.
As an arbitrary example, suppose that I know that the temperature is
200
C and that the state is saturated. The relevant parts of
Table B.1.1 on page 676 of the book are then:
Table B.1.1 (continued)
Saturated Water
In order of appearance, the title tells me that this table is for
``saturated water.'' The table header tells me that the values in the
first column are the temperatures, so I look up the given 200C
in the first column. The entire row I find applies to saturated water
at 200C. For example, the value in the second column tells me
that the pressure is 1553.8 kPa for saturated water at 200C
(the kPa unit is found in the table header for the second column).
The value in the third column tells me that the specific volume of the
saturated water at 200C is 0.001156 m3/kg if it is all in
liquid form (the ``f'' in vf stands for liquid; think
``fluid''). Similarly the value in the fifth column tells me that
the specific volume of saturated water is 0.12736 m3/kg if it is
all in vapor form (the ``g'' in vg stands for vapor; think
``gas''). (The value in in the fourth column I skipped is merely
the difference between the two.)
Similarly, the value in the sixth column tells me the internal energy, used later in the course, if the saturated water is in liquid form, and the eight column shows the one if it is in vapor form. There is more; the row of data extends to the facing page 675, giving enthalpy and entropy, but you get the idea.
We emphasize once more that we need only one piece of information to
find our location in the saturated table. Suppose that instead
of the temperature, we had only been given that the water is saturated at
a pressure of 1553.8 kPa. We would simply have looked up this value
in the second, pressure column, of table B.1.1, and found the exact
same row. Then we could have read off that the temperature was
200C in the table, this need not be given now.
The superheated vapor and compressed liquid tables, however, are
two-dimensional. We need two pieces of information to find our
location in those tables. For example, if we are given that, say, the
temperature of superheated water vapor is 300C and the
pressure is 50 kPa, we turn to table B.1.3 for saturated water vapor,
then we locate the block of data corresponding to 50 kPa on page 682,
top left quarter page, and then we locate the row corresponding to
300C in that block:
Table B.1.3
Superheated Vapor Water
You see that at 300C and 50 kPa, the specific volume
v=5.28391 m3/kg, the internal energy u=2811.33 kJ/kg, the
``enthalpy'' h=3075.52 kJ/kg and the ``entropy'' s=8.5372 kJ/kg-K.
Don't forget to check the units.
In this section, we will determine the phase of a substance, given two intensive variables. Note that we need to determine the phase to figure out what table to use. When we know the table, our two intensive variables should also be enough to read off that table.
Example 1: p=100 kPa and 
C
Suppose we are given that water is at a pressure p=100 kPa and at a
temperature C. We want to figure out what phase the water is
in, which will tell us what table to use.
We will use the Tv-diagram in this example, and the idea is to
sketch both the horizontal 200C isotherm and the broken 100 kPa
isobar. The state we are looking for should be on both of those
lines, since it is both 100 kPa and 200C. To be on both lines, the
state must be the point where they intersect.
The broken-line-first method draws the broken isobar first:
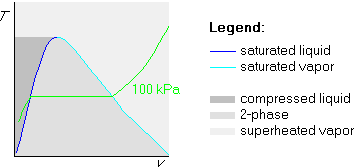
Now, before drawing the 200C isotherm, we need to locate the
temperature of the horizontal part of the isobar. Since the
horizontal part is saturated, we get its temperature by looking up 100
kPa in the saturated table. Looking in table B.1.1 for 100 kPa, we find
that that exact value is not in the table; the closest is 101.3 kPa,
which is close enough. According to table B.1.1, the saturated temperature
at 100 kPa pressure is 100C.
If we want, or need, to be more precise, we can interpolate in table
B.1.1 to exactly 100 kPa. That gives 99.61C. For water, however,
there is a quicker method. The book gives another tabulation of the
saturated data, ``pressure entry'' table B.1.2, for round values of
the pressure. If we look in B.1.2, we immediately see that the
saturated temperature at 100 kPa is 99.62C exactly. Pretty much
the same as we found using interpolation. Note however, that for
substances other than water, no separate ``pressure entry'' table is
available.
In any case, the conclusion is that the temperature of the horizontal part
is 99.62C. Mark it on the T-axis at the height of the horizontal
part of the isobar:
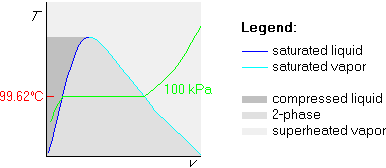
Finally, draw the 200C isotherm. Since 200C is more than
99.62C, we draw the 200C isotherm above the horizontal
part of the isobar:
C
isotherm is the state of the water. We see that it is in the light
grey superheated vapor region.
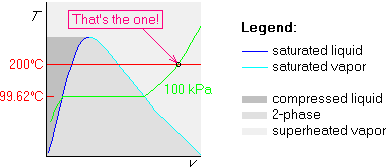
So, we have found the phase: our water is in the superheated vapor phase.
If we want to figure out other intensive variables, say the specific volume, we should use superheated vapor Table B.1.3 to find them. The relevant parts of this table, on page 682 of the book, are then:
Table B.1.3
Superheated Vapor Water
C in the first column. In the column marked v, we then
find that the specific volume v=2.17226 m3/kg.
The reason that we had to look up the temperature of the horizontal,
saturated part of the isobar is that we have to know whether to draw
our isotherm above of below the horizontal part of the isobar. As a
second example demonstrating the difference, assume that the pressure
is again given to be 100 kPa, but the temperature is now given as
40C.
Example 2: p=100 kPa and 
C
The first two steps, drawing the broken isobar and locating its horizontal part, are the same as before:
C is less than 99.62C, we now draw the
isotherm below the horizontal part of the isobar:
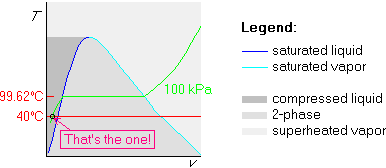
If we actually try to do so, we run into a problem however. The given
pressure of 100 kPa is not in table B.1.4! The lowest pressure in the
table is 500 kPa. Fortunately, if this happens for a compressed
liquid, it is often sufficiently accurate use the saturated value
as an approximation. In the saturated table B.1.1, we find the
specific volume of saturated liquid water to be vf=0.001008
m3/kg at the correct temperature of 40C, but the wrong
pressure of 7.384 kPa. Make sure you get the temperature right.
This saturated value v=0.001008 m3/kg is sufficiently accurate
for our compressed liquid too. Despite the error in pressure.
If you really need a more accurate value for the specific volume, you could interpolate the saturated value at 7.394 kPa that we just read off and the compressed liquid value at 500 kPa from table B.1.4 to find the value at 100 kPa. But in this example, you would still get 0.001008 for the specific volume if you did that.
Note that for substances other than water, the book does not provide a compressed liquid table, and you have no choice other than to use saturated values for the compressed liquid phase.
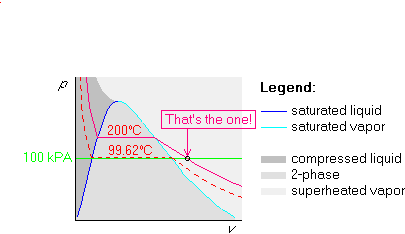
Let us try to redo the first example we did in the previous
subsection. But now, we will use the pv-diagram instead of the
Tv-one. We are again given that water is at a pressure p=100 kPa
and at a temperature T=200C.
Example 1: p=100 kPa and C
The procedure is very similar to the one in the Tv-diagram. Again,
we draw the broken line first, but in the pv-diagram, the broken
line is the isotherm. So we draw the 200C isotherm:
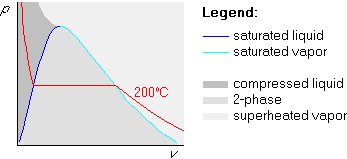
Next we figure out the pressure of the horizontal, saturated part of the
isotherm by looking up 200C in table B.1.1. The saturated pressure
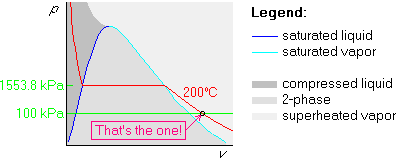
at 200C is there found to be 1553.8 kPa. Mark it in the graph:
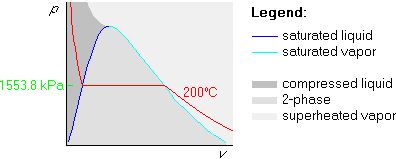
Finally draw the 100 kPa isobar below the horizontal part, since 100 kPa is less than 1553.8 kPa:
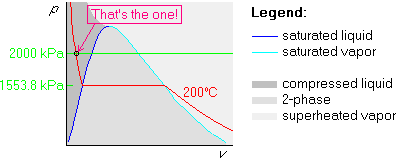
Example 2: p=2000 kPa and C
The first two steps are the same as above, but in the third step, we draw the 2000 kPa isobar above the horizontal part, since 200 kPa is greater than 1553.8:
C isotherm
is seen to be in the compressed liquid table.
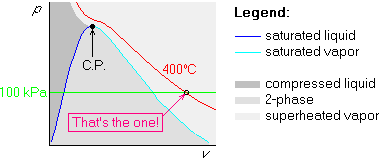
Example 3: p=100 kPa and 
C
If we try to repeat the procedure of examples 1 and 2 immediately
above, we run into trouble. The given value of the temperature is
higher than the highest temperature in table B.1.1. The top of the
two-phase region is known as the critical point, (C.P.), and its
temperature is 374.1C for water. The given temperature of 400C
is higher than that, so it will never enter the two-phase region.
If this happens, simply draw the isotherm to stay above the two-phase region; the rest is unchanged:
C is seen to be
superheated vapor.
Sometimes it is more convenient to draw the straight isoline first. For example, if you are locating several states in the Tv-diagram, all with the same temperature, it is quicker and neater to draw this constant temperature line first.
Example 1: p=100 kPa and 
C
In this method, we first draw the straight 50C isotherm:
Now the trick is to find out what isobar coincides with this isotherm
in the two-phase region. So, we look up 50C in table B.1.1, and find
that its saturated pressure is 12.35 kPa. We can now draw this isobar
as a dotted line:
C isotherm in the two
phase region.
Finally, we draw the 100 kPa isobar. Since 100 kPa is greater than 12.35 kPa, we draw the 100 kPa isobar above the 12.35 kPa isobar:
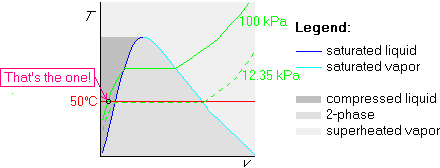
Example 2: Also determine p=5 kPa and C
Since the temperature is again 50C, we can use the same graph as
above and simply add the 5 kPa isobar. Since 5 kPa is less than 12.35
kPa, we draw it below that isobar:
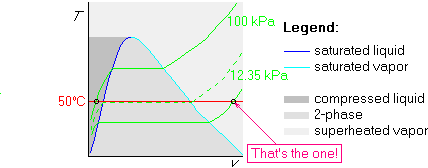
Note that we only needed to do one table look up, for 50C, to do
the figure. Using the broken-line-first method, we would have had to
do two table look ups, one for the constant part of each isobar.
This goes very similar.
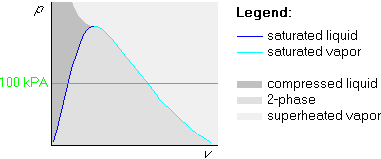
Example 1: p=100 kPa and C
We draw the straight 100 kPa isobar:
C isotherm. Draw it
as a dotted line:
C isotherm:
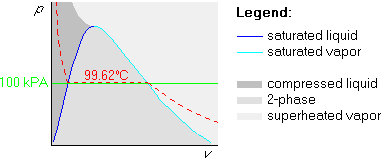
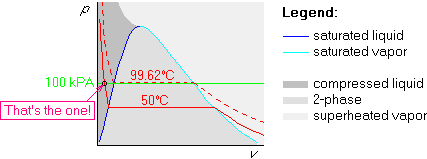
Example 2: p=100 kPa and C
The first two steps are the same as above, but the 200C isotherm
is above the 99.62C one:
If p and v are given, it is fairly obvious you want to use the pv-diagram to find the phase.
Example 1: p=500 kPa and v=0.001 m3/kg
First draw the horizontal isobar that represents all states with the given pressure of 500 kPa:
Finally draw the isochore with the given specific volume v = 0.001 m3/kg in the pv-diagram. Since 0.001 m3/kg is less than the saturated fluid value vf = 0.001093 m3/kg, this isochore will be before (i.e. to the left of) the vf one:
Example 2: p=500 kPa and v=0.1 m3/kg
This is just like example 1, except that the given v=0.1 m3/kg is now in between vf = 0.001093 m3/kg and vg = 0.37489 m3/kg. So the v=0.1 m3/kg isochore is in between those two:
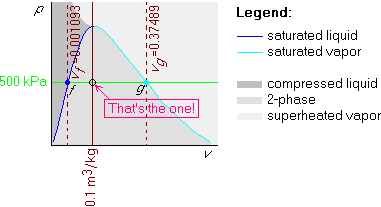
You can immediately look up the temperature in the saturated table
B.1.2; it is 151.86C. To get the quality x, use
Example 3: p=500 kPa and v=1 m3/kg
This is again just like example 1, except that the given v=1 m3/kg is now greater than vg = 0.37489 m3/kg. So this isochore is towards the left of that line:
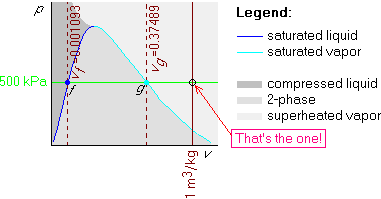
Getting the phase from T and v works exactly like getting the phase from p and v, except that you now use the Tv-diagram and temperatures instead of pressures.
If T and x are given, the obvious diagram to use is the Tv-diagram. Let's decide right away that if x is given, the phase can never be compressed liquid or superheated vapor, because x is not defined for those phases.
Example 1: Saturated liquid at C
Telling you that the water is saturated liquid is equivalent to telling you that x=0. Since we are saturated, the pressure is 12.35 kPa from table B.1.1.
The state is on both the 50C isotherm and on the dark blue
saturated liquid line:
Example 2: Saturated vapor at C
Telling you that the water is saturated vapor is equivalent to telling you that x=1. Since we are saturated, the pressure is 12.35 kPa from table B.1.1.
The state is on both the 50C isotherm
and on the light blue saturated vapor line:
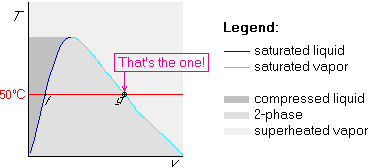
Example 3: x=0.25 and C
Since x=0.25, one quarter of the water is saturated vapor, and the remaining three quarters saturated liquid. Since we are saturated, the pressure is 12.35 kPa from table B.1.1.
The state is on the 50C line, one quarter of the way between the
saturated liquid and saturated vapor states:
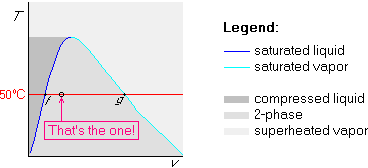
v = vf + x (vg-vf)
Getting the phase from p and x works exactly like getting the phase from T and x, except that you now use the pv-diagram and pressures instead of temperatures.
As you have seen, the procedures vary a lot depending on the diagram used and what variables are given. But in every case, after we have drawn the first given isoline, we use the saturated tables to find out something more about that isoline before we draw the second given isoline.
Later in the course additional intensive variables such as the internal energy u, the enthalpy h, and entropy s are encountered. In case one of those is one of the two given intensive variables, they behave much like v does. As a rule, treat them as you would v.
Example: p=100 kPa and u=1000 kJ/kg
Since the given u is in between the uf=417.33 kJ/kg and ug=2506.06 kJ/kg values of table B.1.2 at 100 kPa, the water is two-phase, saturated liquid plus saturated vapor. Compute x from
u = uf + x (ug-uf)
then compute the specific volume, say, fromv = vf + x (vg-vf)
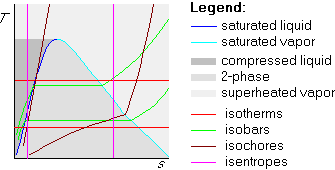
where vf and vg are in the table.Later in the course, we encounter entropy s as another intensive variable. Plotting temperature versus entropy is often desirable, giving the Ts-diagram. A sketch of its features is:
We can also draw isentropes in the pv-diagram. They are not vertical like in the Ts-diagram, but they do go down quite steeply:
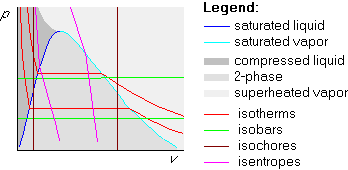
Isentropes and isotherms are the building blocks of the Carnot cycle. A Carnot cycle is always a rectangle in the Ts-diagram. In the pv-diagram, it is not; the actual shape there depends a lot on whether part or all of the cycle is in the two-phase region.