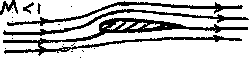Flow around thin airfoils.

  An example physical context which shows how the differences between different types of differential equations reflect in physical systems is the flow around thin airfoils. The governing partial differential equation is

 

(1 - M²) u_xx + u_yy = 0,

where M is the Mach number at which the airfoil is flying, and u can respresent any characteristic quantity such as the pressure, the velocity potential, or a velocity component.

For Mach numbers less than 1, corresponding to subsonic flow, the partial differential equation is elliptic. It becomes the Laplace equation when the Mach number is negligible. On the other hand, for Mach numbers greater than one, corresponding to supersonic flight, the equation is the hyperbolic wave equation. (The equation is not valid for Mach numbers close to unity.)

The differences in the appearance of the solution reflects the difference in the type of partial differential equation. For subsonic, elliptic conditions, the solution is very smooth as shown in figure 16. The influence of the airfoil is felt everywhere, even in front of it.

  

Figure 16: Subsonic flow around a thin airfoil.

In contrast, for the supersonic case, the flow contains singularities in the form of shocks and expansion fans. There are kinks in the streamlines at the shocks, and jumps in the curvature of the streamlines at the expansion fans. The influence of the airfoil is further not felt upstream of the front shock.

  

Figure 17: Supersonic flow around a thin airfoil.

To compute the supersonic flow, we could start a computation at the leading edge of airfoil. We could compute the flow along vertical lines, a line at a time, working backwards, and we could stop when we have reached the trailing edge. In fact, we can even write down an analytical solution, by identifying the functions u_R and u_L in (14) using the boundary conditions on the airfoil.

For the subsonic case however, we would define a mesh that extends sufficiently far away from the airfoil in all directions. Then we would solve for the flow at all mesh points at the same time, possibly using an iterative procedure. Clearly, this is more awkward than the supersonic case. There are other approaches we could take, especially for a thin airfoil, but none as simple and elegant as for the supersonic case.