Next: About properly posed
Up: The Laplace equation.
Previous: The boundary conditions.
Mathematically the difference between the wave equation and the
Laplace equation is only a minus sign in the second term, but this
makes a great difference. While the wave equation propagates
singularities, the Laplace equation, like the heat equation, smooths
them out. For the example, while at the lower boundary of the plate
the temperature has a jump from 100 to zero degrees, in the interior
this singularity disappears. Two temperature profiles, one at the
lower boundary and one a bit inside the plate, are shown in
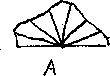
figure 13. Figure 14 shows the
shape of the isotherms in the plate near the jump in the boundary
condition. At the jump, the temperature is multiple-valued,
but away from the boundary, the isotherms fan out into a smooth
solution. Clearly, solutions of elliptic equations such as the
Laplace equation look very different from solutions of hyperbolic
equations such as the wave equation.
Figure 13:
Smoothing of a singularity.
 |
Figure 14:
Smoothing of a singularity.
 |
Next: About properly posed
Up: The Laplace equation.
Previous: The boundary conditions.
