5.8 An alternate procedure

This example tries to be clever about handling inhomogeneous boundary equations for the Laplace equations. It does run into a few problems. But the students will of course explain and fix up the problem.

5.8.1 The physical problem

Find the steady temperature distribution in the square plate/cross section below if the heat fluxes out of the sides are known.

$$\hbox{\epsffile{sva1.eps}}$$

5.8.2 The mathematical problem

$$\hbox{\epsffile{sva2.eps}}$$

• Finite domain $\bar \Omega$: $0\le x \le 1$, $0\le y \le 1$.
• Unknown temperature $u=u(x,y)$
• Elliptic
• Four Neumann boundary conditions
• Integral constraint due to all Neumann boundary conditions:
  
  $$\int_0^1 p(x){ \rm d}x - \int_0^1 g(y){ \rm d}y - \int_0^1 q(x){ \rm d}x + \int_0^1 f(y){ \rm d}y = 0$$
  
  

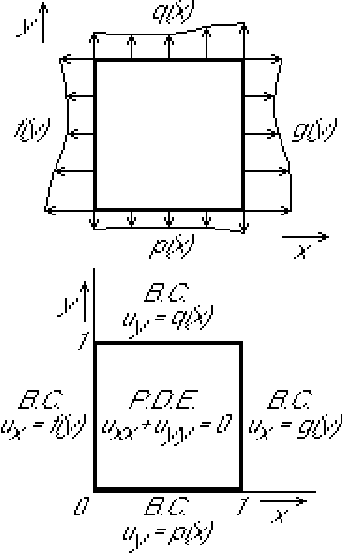
Try separation of variables:

$$\sum_n u_n(y) X_n(x) \hbox{ or } \sum_n u_n(x) Y_n(y)$$

5.8.3 Step 0: Fix the boundary conditions

$$\hbox{\epsffile{sva2.eps}}$$

Standard approach:

All boundary conditions are inhomogeneous. Our standard approach would be to set $u=u_0+v$ where

$$u_{0x}(0,y)=f(y) \qquad u_{0x}(1,y)=g(y)$$

and then set

$$v = \sum_n v_n(y) X_n(x)$$

This would work without any problems. A $u_0$ quadratic in $x$ would be fine. Of course, this choice for $u_0$ is quite arbitrary.

Alternative approach:

Instead, we will follow a more elegant procedure that does not require us to arbitrarily choose a $u_0$. Unfortunately, this alternative procedure will get us into some trouble.

The idea is that the given problem can be seen as the sum of two problems, each with homogeneous boundary conditions in one direction.

$$\hbox{\epsffile{sva3.eps}}$$

If we add the solutions $u$ to the two problems together, we should get the solution to the original problem.

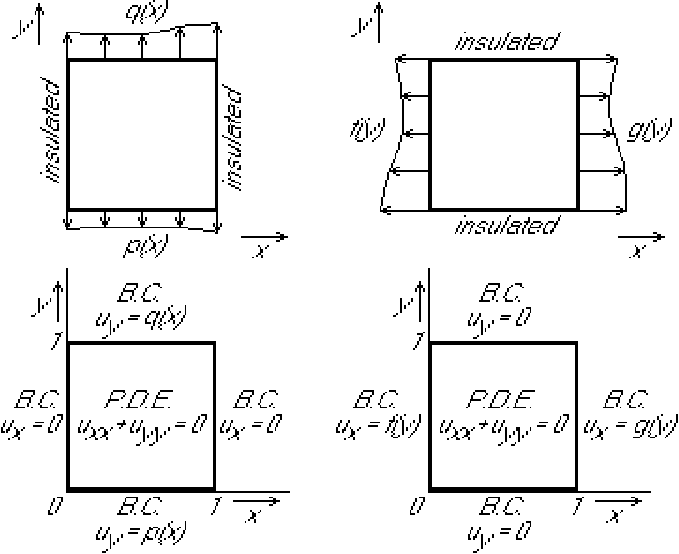
The instructor will solve the left hand problem. The students will solve the right hand problem, identify the difficulty, and fix it.

Some people split up the problem into 4, one for each side. That makes the difficulty even worse.

5.8.4 Step 1: Find the eigenfunctions

Substitute $u=T(y) X(x)$ into the homogeneous partial differential equation $u_{xx} + u_{yy} = 0$:

$$TX'' + T'' X = 0$$

$$\frac{T''}{T} = - \frac{X''}{X} = \hbox{ constant } = \lambda$$

Since the instructor's $x$-boundary conditions are homogeneous, he has a Sturm-Liouville problem for $X$:

$$- X'' = \lambda X \qquad X'(0) = 0 \qquad X'(1)=0$$

This was already solved in problem 7.19. Looking back there, substituting $\ell=1$,

$$\lambda_n = n^2 \pi^2 \qquad X_n = \cos\left(n \pi x\right) \qquad (n = 0, 1, 2, 3, \ldots)$$

5.8.5 Step 2: Solve the problem

Expand all variables in the problem for $u$ in a Fourier series:

$$\hbox{\epsffile{sva3.eps}}$$

$$u = \sum_{n=0}^\infty u_n(y) X_n(x) \quad p(x) = \sum_{n... ...\infty p_n X_n(x) \quad q(x) = \sum_{n=0}^\infty q_n X_n(x)$$

$$p_n = \frac{\int_0^1 p(x) X_n(x){ \rm d}x}{\int_0^1 X^2_n(x){ \rm d}x}$$

$$q_n = \frac{\int_0^1 q(x) X_n(x){ \rm d}x}{\int_0^1 X^2_n(x){ \rm d}x}$$

Remember that the expression you find for the integrals in the bottom, $\frac12$, does not work for $n=0$, in which case it turns out to be $1$.

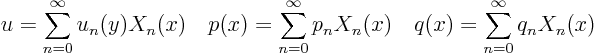
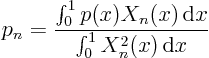
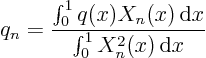
Fourier-expand the partial differential equation $u_{xx} + u_{yy} = 0$:

$$\sum_{n=0}^\infty u_n(y) X_n(x)'' + \sum_{n=0}^\infty u_n(y)'' X_n(x) = 0$$

Because of the Sturm-Liouville equation in the previous section

$$- \sum_{n=0}^\infty \lambda_n u_n(y) X_n(x) + \sum_{n=0}^\infty u_n(y)'' X_n(x) = 0$$

giving the ordinary differential equation

$$u_n(y)'' - \lambda_n u_n(y) = 0$$

or substituting in the eigenvalue

$$u_n(y)'' - n^2 \pi^2 u_n(y) = 0$$

Fourier-expand the boundary condition $u_y(x,0) = p(x)$:

$$\sum_{n=0}^\infty u_n(0)' X_n(x) = \sum_{n=0}^\infty p_n X_n(x) \quad\quad\Rightarrow\quad\quad u_n'(0) = p_n$$

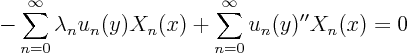
Fourier-expand the boundary condition $u_y(x,1) = q(x)$:

$$\sum_{n=0}^\infty u_n(1)' X_n(x) = \sum_{n=0}^\infty q_n X_n(x) \quad\quad\Rightarrow\quad\quad u_n'(1) = q_n$$

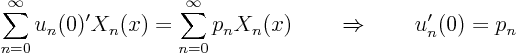
Solve the above ordinary differential equation and boundary conditions for $u_n$. It is a constant coefficient one, with a characteristic equation

$$k^2 - n^2 \pi^2 = 0$$

Caution! Note that both roots are the same when $n=0$. So we need to do the $n=0$ case separately.

For $n \ne 0$ the solution is

$$u_n = A_n e^{n\pi y} + B_n e^{-n\pi y}$$

The boundary conditions above give two linear equations for $A_n$ and $B_n$:

$$\left( \begin{array}{cc\vert c} n\pi & - n\pi & p_n \\... ...pi e^{n\pi} & - n\pi e^{-n\pi} & q_n \end{array} \right)$$

that are best solved using Gaussian elimination. Rewriting the various exponentials in terms of sinh and cosh, the solution for the Fourier coefficients of $u$ except $n=0$ is:

$$u_n = - \frac{{\rm cosh}(n\pi[y-1])}{n\pi{\rm sinh}(n\pi... ...h}(n\pi y)}{n\pi{\rm sinh}(n\pi)}q_n \quad (n=1,2,3,\ldots)$$

For $n = 0$ the solution of the ordinary differential equation is

$$u_0 = A_0 + B_0 y$$

Put in the boundary conditions to get equations for the integration constants $A_0$ and $B_0$:

$$u_0'(0) = B_0 = p_0 \qquad u_0'(1) = B_0 = q_0$$

Oops! We can only solve this if

$$p_0 = q_0$$

Looking above for the definition of those Fourier coefficients, we see we only have a solution if

$$\int_0^1 p(x){ \rm d}x = \int_0^1 q(x){ \rm d}x$$

Unfortunately, these two integrals will normally not be equal! Also, $A_0$ remains unknown.

5.8.6 Summary of the solution

First compute the Fourier coefficients of the given boundary conditions:

$$p_0 = \int_0^1 p(x){ \rm d}x \qquad p_n = 2 \int_0^1 p(x) \cos(n\pi x){ \rm d}x \quad (n=1,2,\ldots)$$

$$q_0 = \int_0^1 q(x){ \rm d}x \qquad q_n = 2 \int_0^1 q(x) \cos(n\pi x){ \rm d}x \quad (n=1,2,\ldots)$$

Then the solution is equal to:

$$\begin{array}{l} \displaystyle u_{\strut} = A_0 + p_0 ... ...pi{\rm sinh}(n\pi)}q_n \right] \cos(n\pi x) \end{array}$$

But this only satisfies the boundary condition on the top of the plate if

$$\int_0^1 q(x){ \rm d}x = \int_0^1 p(x){ \rm d}x$$

No problem! Students will explain and fix the problem.