|
|
|
|
|
Next: 5. Separation of Variables |
|
If ![]() is restricted by finite boundaries, the D'Alembert solution
does not really apply. To use it anyway, we must somehow extend the
problem to a doubly infinite
is restricted by finite boundaries, the D'Alembert solution
does not really apply. To use it anyway, we must somehow extend the
problem to a doubly infinite ![]() -range without boundaries. But our
solution without boundaries should still satisfy the boundary
conditions for the finite range. That is often possible by clever use
of symmetry. An example can clarify that.
-range without boundaries. But our
solution without boundaries should still satisfy the boundary
conditions for the finite range. That is often possible by clever use
of symmetry. An example can clarify that.
The problem is to find the pressure for sound wave propagation in a
tube with one end closed and one end open:
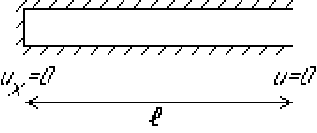
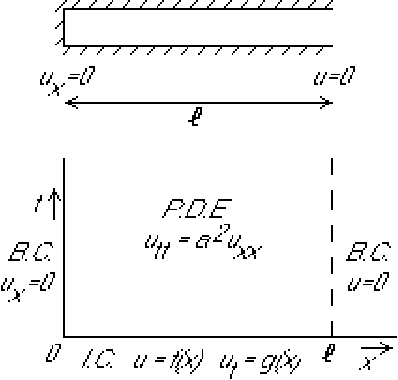
The D'Alembert solution applies to an infinite domain
![]() . So to use the D'Alembert solution, the given
initial conditions, that are valid for
. So to use the D'Alembert solution, the given
initial conditions, that are valid for ![]() must be extended to
all
must be extended to
all ![]() . In other words, functions
. In other words, functions ![]() and
and ![]() must be
converted into functions
must be
converted into functions ![]() and
and ![]() that have
values for all
that have
values for all ![]() . Of course, in the interval
. Of course, in the interval ![]() , they must
stay the same as
, they must
stay the same as ![]() and
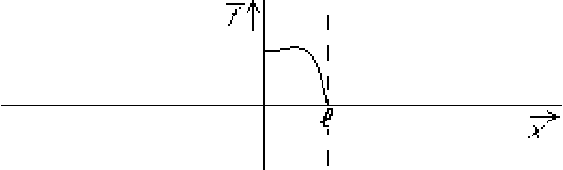
and ![]() . Assume now for example that
. Assume now for example that
![]() looks as sketched below:
looks as sketched below:
You might think that you could now simply take ![]() to be zero
for all
to be zero
for all ![]() outside the range of the pipe. The corresponding
D'Alembert solution will satisfy the wave equation everywhere,
including inside the pipe
outside the range of the pipe. The corresponding
D'Alembert solution will satisfy the wave equation everywhere,
including inside the pipe ![]() . That is good, because the wave
equation must indeed be satisfied. Unfortunately, the solution you
get that way will not satisfy the boundary conditions at
. That is good, because the wave
equation must indeed be satisfied. Unfortunately, the solution you
get that way will not satisfy the boundary conditions at ![]() and
and
![]() . So it will still be wrong.
. So it will still be wrong.
You must select the extension ![]() of
of ![]() to all
to all ![]() so that the correct boundary conditions become automatic.
so that the correct boundary conditions become automatic.
The way to do it is as follows:
The process is shown for ![]() below:
below:
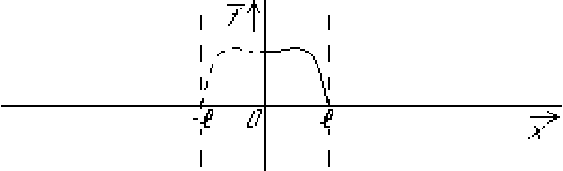
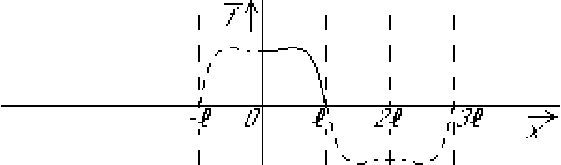
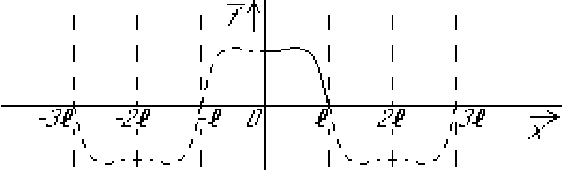
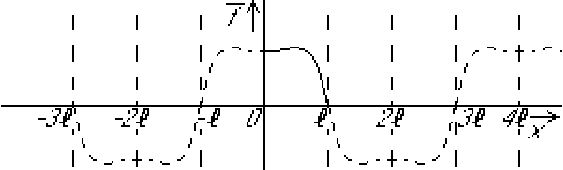
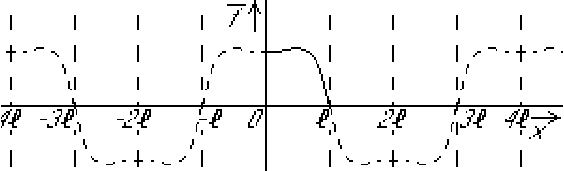
It is OK if you get kinks or discontinuities in your functions ![]() and
and ![]() while creating (anti)symmetry. This happens when
while creating (anti)symmetry. This happens when ![]() and/or
and/or ![]() does not satisfy the given boundary conditions. While then
does not satisfy the given boundary conditions. While then
![]() or
or ![]() may not have a unique value at the initial time, that
problem will disappear when the time becomes greater than zero.
may not have a unique value at the initial time, that
problem will disappear when the time becomes greater than zero.
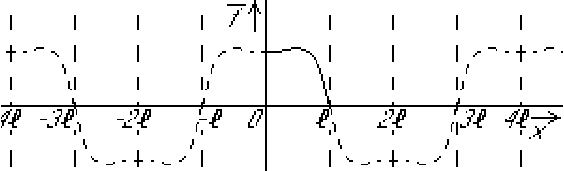
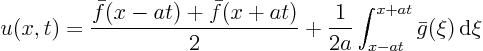

In the range ![]() , the found solution is exactly the same
as for the finite pipe! The solution outside that range can simply be
ignored.
, the found solution is exactly the same
as for the finite pipe! The solution outside that range can simply be
ignored.