3.3 Analytical solution

Often, you want an analytical expression for the solution $u$ of a first order equation in terms of $x$ and $y$. Solving the differential equations gives expressions valid along characteristic lines, which is not the same thing. These expressions involve two integration “constants”, call them $C_1$ and $C_2$, that themselves are unknown functions of $x$ and $y$: if you move from one characteristic line to another, the values of $C_1$ and $C_2$ will normally change. They are only constants along the characteristic lines.

To get a relationship for $u$ as a function of $x$ and $y$, the trick is to recognize that there is a functional dependence between the two integration constants involved. You can use, say, $C_1$ as a label for what characteristic curve you are on: different values of $C_1$ correspond to different characteristic lines. And $C_2$ only depends on what characteristic line you are on, not on the position on the line. So $C_2$ only depends on what $C_1$ is; $C_2$ is some function $C_2(C_1)$ of $C_1$. What function that is remains unknown; that depends on the relevant initial or boundary condition, but it is some function.

The procedure to find $u$ as a function of $x$ and $y$, or at least, to find the most general and precise expression between these three quantities, is therefor:

1. In one of the two ordinary differential equation solutions you obtained, say the one involving the integration constant you called $C_2$, replace $C_2$ by the more precise $C_2(C_1)$ to indicate that it is not really a constant, but still depends on what $C_1$ is.
2. Substitute for $C_1$ from the other ordinary differential equation solution.

Note that in some special cases, it makes a difference in which of the two ordinary differential equation solutions you take the integration constant to be a function of the other one: sometimes $C_2(C_1)$ is not a well-defined function, but $C_2(C_1)$ is. (An example is in subsubsection 3.5.5.)

Example

Question: (5.30 continued) Solve

$$y u_x + x u_y = cu$$

Solution:

Previously, it was found that the characteristics of this example were given by

$$u = C_2 (x+y)^c \qquad\mbox{along a characteristic}\qquad y^2 = x^2 + C_1$$

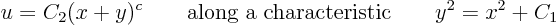
To get the general expression for $u(x,y)$, first note that more precisely,

$$u = C_2(C_1) (x+y)^c,$$

then plug in the expression for $C_1$ from the other equation to get

$$u(x,y) = C_2(y^2 - x^2) (x+y)^c.$$

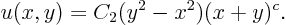
This is the most general solution of the partial differential equation. Function $C_2()$ remains undetermined; the above expression is a solution of the partial differential equation regardless what one-argument function you take for $C_2()$.

In fact, you need an undetermined one-argument function in the solution, because you must still match the function used to specify the relevant initial or boundary condition, also a one-argument function.