1.2.3.5 Solution stanexw-f

Question:

Find the possible plane wave solutions for the two-dimensional wave equation

$$u_{tt} = a^2 u_{xx} + a^2 u_{yy}$$

What is the wave speed?

Also find the possible standing wave solutions. Assume homogeneous Dirichlet or Neumann boundary conditions on some rectangle $0<x<\ell$, $0<y<h$. What is the frequency?

Repeat for the generalized equation

$$u_{tt} = a_1^2 u_{xx} + a_2^2 u_{yy} + b^2 u$$

where $a_1$, $a_2$, and $b$ are positive constants.

Answer:

Plane wave solutions are solutions of the form

$$u= f(\vec n \cdot\vec x- ct)$$

where $c$ is a constant, giving the speed of the wave, and $\vec{n}$ a constant unit vector, giving the direction of propagation.

Plugging it into the wave equation produces $c^2=a^2$ so the propagation speed is $\pm{a}$. The “wave shape,” the function $f$, is completely arbitrary.

These are propagating two-dimensional waves. To make this point, you can show a picture of the wave at both time zero and at a time $t>0$, assuming an arbitrary wave shape $f$

There is an alternate solution in which the wave speed is completely arbitrary but the wave shape is not. Since this solution is not bounded, you can argue that it is not what people usually understand to be a wave. You might compare its wave shape with waves on the beach, for example.

If you plug the general expression for a plane wave into the generalized wave equation, things change. You find an ordinary differential equation for the wave shape. You find that that equation has only finite solutions if

$$\vert c\vert < \sqrt{a_1^2 n_x^2+a_2^2 n_y^2}$$

In that case, you find that the waves are sinusoidal:

$$u = A \sin(k[n_xx+n_yy]+\phi)$$

where the amplitude $A$ and the phase angle $\phi$ are arbitrary constants. The wave speed $c$ is related to the wave number $k$ as

$$c = \pm\sqrt{a_1^2n_x^2+a_2^2n_y^2 - \frac{b^2}{k^2}}$$

Therefore, when $b$ is not zero, the sinusoidal waves in a given direction do not all go at the same speed as they do for the basic wave equation. In particular, waves of smaller wave number, or longer wave length, go slower. And at a lowest value of the wave number, the waves come to a halt. Below that wave number, there are no propagating sinusoidal waves.

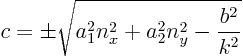
The standing wave solutions of interest are solutions of the form

$$u = \sin(k_x x +\phi_1)\sin(k_y y+\phi_2) \sin(\omega t+\phi_3)$$

where the wave numbers $k_1$ and $k_2$, and the frequency $\omega$ are positive constants. These can satisfy homogeneous Dirichlet or Neumann boundary conditions on some rectangle $0<x<\ell$, $0<y<h$. The phase angles $\phi$ are not important here so you may assume them to be zero.

Use a sketch at different times to show that the shape of the wave does not change. Only the amplitude changes. The wave does not move; for example, draw attention to the locations where $u=0$.

If you plug it in, for the standard wave equation you find $\omega =\pm{a}k$ where $k=sqrt{k_x^2+k_y^2}$. The ratio $\omega /k$ is therefore equal to the wave speed $a$ in magnitude.

For the generalized wave equation, there are only standing wave solutions if the wave number is large enough. In particular you find that if $a_1=a_2=a$, then $k>b/a$ is required.