1.2.3.3 Solution stanexw-c

Question:

Consider the following wave equation problem in a unit square:

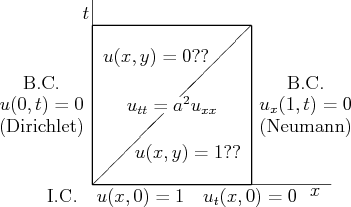
This is basically identical to a Laplace equation problem in the first subsection. Like that problem, the above wave equation problem has a unique solution. It is relevant to a case of acoustics in a tube, with $u$ the pressure. Someone proposed that the solution should be simple: in the upper triangle the solution $u(x,t)$ is 0, and in the lower triangle, it is 1.

Thoroughly discuss this proposed solution. Find out whether the boundary conditions and initial conditions are satisfied. Is the partial differential equation satisfied in both triangles? Finally discuss whether the solution is right. Consider the value of the wave speed $a$ in your answer.

Sketch the isobars of the correct solution. In particular, sketch the $u=0$ 0.25, 0.5, 0.75, and 1 isobars, if possible. Sketch both the case that $a=1$ and that $a=\sqrt{2}$.

Answer:

Plug the given two-region solution into the partial differential equation, boundary, and initial conditions to verify that they are satisfied.

However, singularities should propagate with the wave speed. Show that the speed of propagation ${\rm d}{x}/{\rm d}{t}$ of the singularity is one. So argue that the solution can only be right for $a=1$.

Draw the 0.25, 0.5, and 0.75 at the locations where the solution changes from 0 to 1, apparently passing through 0.25, 0.5, and 0.75 while doing so.

Argue that an entire region has $u=0$ and that a region cannot be drawn as a single line. Similarly for $u=1$.

Obviously, for $a=\sqrt 2$ the singularity must propagate with that speed. Use that to produce your correct isobars.