1.2.1.7 Solution stanexl-c

Question:

Consider the following Laplace equation problem in a unit square:

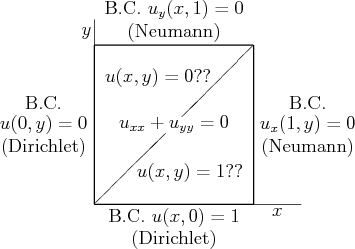
The problem as shown has a unique solution. It is relevant to a case of heat conduction in a square plate, with $u$ the temperature. Someone proposed that the solution should be simple: in the upper triangle the solution $u(x,t)$ is 0, and in the lower triangle, it is 1.

Thoroughly discuss this proposed solution. Find out whether the boundary conditions and initial conditions are satisfied. Is the partial differential equation satisfied in both triangles?

Explain why all isotherms except 0 and 1 coincide with the 45$\DG9/$ line. And why the zero and 1 isotherms are indeterminate.

Finally discuss whether the solution is right.

Answer:

Plug the two given expressions for $u$ into the Laplace equation and boundary conditions. Show that they are satisfied.

An entire triangle has temperature 0, and the inside of a triangle cannot be shown as a single line. The same for temperature 1.

Finally, show that the solution has a jump singularity inside the plate. That is inconsistent with the requirement that solutions of the Laplace equation are smooth inside the considered region. That means that the solution is no good.