|
|
|
|
Skip to: 1.2.1.6 Solution stanexl-b5 |
|
Consider the Laplace equation within a unit circle, but now in polar coordinates:
The solution is the Poisson integral formula
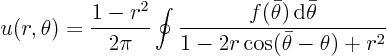
Now suppose that function ![]() is increased slightly, by an amount
is increased slightly, by an amount ![]() , and only in a very small interval
, and only in a very small interval
![]() .
.
Does the solution ![]() change everywhere in the circle, or only in the immediate vicinity of the interval on the boundary at which
change everywhere in the circle, or only in the immediate vicinity of the interval on the boundary at which ![]() was changed. What is the sign of the change in
was changed. What is the sign of the change in ![]() if
if ![]() is positive?
is positive?
Answer:
To simplify this, assume that the new solution is
![]() where
where ![]() is the old solution. So
is the old solution. So ![]() is the change in the solution.
is the change in the solution.
You now have for the original solution
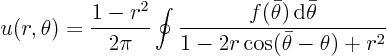
![\begin{displaymath}
u(r,\theta)+\delta u(r,\theta) = \frac{1-r^2}{2\pi} \oint\fr...
...theta)]{ \rm d}\bar\theta} {1-2r\cos(\bar\theta -\theta)+r^2}
\end{displaymath}](img55.gif)
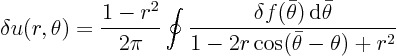
Now
![]() is only nonzero in the interval from
is only nonzero in the interval from ![]() to
to ![]() , so
, so
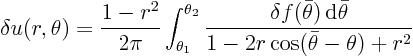
Now use a little graph to show that for any point not extremely close to the segment from ![]() to
to ![]() on the boundary, the denominator of the integrand is about constant, so
on the boundary, the denominator of the integrand is about constant, so

Now show that
Then argue that this means that ![]() is positive everwhere inside the circle. So the region of influence of the little segment is the interior of the circle, and the temperature increases everywhere.
is positive everwhere inside the circle. So the region of influence of the little segment is the interior of the circle, and the temperature increases everywhere.