1.2.1.3 Solution stanexl-b1

Question:

Consider the Laplace equation within a unit circle:

$$u_{xx} + u_{yy} = 0 \qquad\mbox{for}\qquad x^2+y^2<1$$

The boundary condition on the perimeter of the circle is

$$u = (y^2 + 1) x \qquad\mbox{for}\qquad x^2+y^2=1$$

To find the value of $u$ at the point (0.1,0.2), can I just plug in the coordinates of that point into the boundary condition?

There is a symmetry argument that you can give to show that $u$ is zero on the entire $y$-axis $x=0$. What?

Answer:

First verify that the given boundary condition expression, $u=(y^2+ 1)x$ does not satisfy the Laplace equation. So this expression is not valid for $u$ inside the circle.

Of course, the value for $u$ at the given point might still be right by coincidence. To check that, first verify that the correct solution to the problem is

$$u={\textstyle\frac{5}{4}} x + \frac 34 x y^2 - {\textstyle\frac{1}{4}} x^3$$

Do so by plugging it into the partial differential equation and boundary condition. Then compute the value of $u$ at the given point and compare with what you would get from the given boundary condition.

To show that $u=0$ at $x=0$, you want to show that $u$ is an antisymmetric function of $x$. That means that you want to show that

$$u(-x,y) = - u(x,y)$$

That is enough to show that $u$ is zero at $x=0$, because it implies that $u(0,y)=-u(0,y)$. Something can only be equal to its negative if it is zero.

It is quite self-evident that $u$ will be antisymmetric in $x$ because:

• The given boundary condition is antisymmetric in $x$.
• The Laplace equation preserves the antisymmetry: if you take two $x$-derivatives of an antisymmetric function, you get again an antisymmetric function. For example, two derivatives of $\sin(x)$, an antisymmetric function, produces $-\sin(x)$, again an antisymmetric function.

However, saying that something is self-evident and proving it rigorously are different things. To prove it, define a couple of new variables:

$$\bar x = -x \qquad\bar u(\bar x, y) = - u(x,y)$$

Here $\bar{x}$ is the $x$-coordinate flipped over around the $y$-axis, and $\bar{u}$ is $u$ with its sign flipped over.

Graphically, this may be pictured as follows:

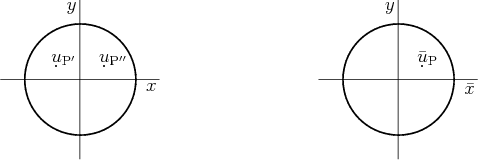
In terms of this picture, $\bar{u}$ at a point P in the $\bar{x},y$-plane is defined as $-u$ at the point P' in the $x,y$-plane.

Show that $\bar{u}(\bar{x},y)$ satisfies the Laplace equation just like $u(x,y)$. Show that $\bar{u}(\bar{x},y)$ satisfies the exact same boundary condition as $u(x,y)$, (in terms of $\bar{x}$ of course.) Since Dirichlet boundary value problems for the Laplace equation have unique solutions, $\bar{u}(\bar{x},y)$ is the exact same function as $u(x,y)$. In terms of the picture above, $\bar{u}$ at the point P is the same as $u$ at the point P''. Since it is also equal to $-u$ at P', it follows that $u$ at P' is $-u$ at P''. So $u$ is antimsymmetric.