 (Click the picture to see a larger version of it).
(Click the picture to see a larger version of it).
Work performed with Shan-fu Shen. This work was made possible by support of the Air Force Office of Scientific Research.
This document gives an history of the discovery of `unsteady boundary layer separation.'
Boundary layer separation is one of the most important factors
that determines how well airplanes, ships, cars, engines, bridges,
modern wind mills, and so on, function.
Scientists have historically been using a circular cylinder as a simplified
`vehicle' to try to understand what is going on.
For example, around the beginning of this century,
the German scientists
Ludwig Prandtl
and
H. Blasius
studied the boundary layer that develops when a cylinder starts to move.
By experiments and innovative mathematics,
they proved that a boundary layer initially forms right next to the
surface of the moving cylinder. It is a layer affected by
friction with the surface of the cylinder:
 (Click the picture to see a larger version of it).
(Click the picture to see a larger version of it).
Prandtl and Blasius believed that this boundary layer would eventually separate from the surface; for typical practical applications this would have disastrous effects for aerodynamic resistance, lifting capability, stability, etcetera.
At that time, it was not clear exactly what would cause the first separation of the boundary layer from the surface. Prandtl and Blasius assumed it would occur when the boundary layer developed an internal layer next to the surface; in this layer the air or water would rotate in the opposite direction from the rest of the boundary layer. Separation would occur at the start of the internal layer.
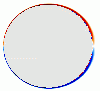
Nowadays we can perform a computation of the flow and make the sense of rotation visible using different colors. That is done in the previous picture; take another look at it. In the picture, the cylinder has moved over a distance equal to half its diameter.
The picture shows that Prandtl and Blasius were right in that internal layers of different colors form; they are visible at the right hand (leeward) side of the cylinder. According to Prandtl and Blasius, separation should occur at the leftmost points of these layers. In fact, it should already occur much earlier, as soon as the cylinder has moved over one sixth of its diameter. The difficulty is that not much seems to be happening with regard to separation of the boundary layer from the surface. (The idea of Prandtl and Blasius turned out to be useful for later times, when the boundary layer separation has had time to develop fully.)
It was in the latter part of the fifties that fluid dynamicist such as Frank Moore, Nicholas Rott, and Bill Sears really started noting that the internal sublayer does not need to mean separation. Something better was needed to decide whether the boundary layer was truly separating from the surface. Moore and later more strongly Sears & Telionis developed the idea that `singularities in the boundary layer equations' were the way to diagnose separation.
This requires a bit of explanation. The boundary layer equations had been discovered by Ludwig Prandtl in 1904 as approximate equations to compute the flow in thin boundary layers. Through the work of Sidney Goldstein of England in 1948, it had become likely that the solution to these equations stops to exist when the boundary layer separates. The point at which the solution stops to exist is called a singularity.
In short, if the ideas of Sears & Telionis were to be correct, there would have to be a singularity in the boundary layer equations for the circular cylinder. This was certainly an interesting assumption, but there was one major difficulty: numerical solutions were already available, and they did not show any singularity! The solution just seemed to be going on forever, without terminating.
At first, there were some suggestions that a singularity had been overlooked in the earlier computations, but these claims were never verified by later authors. Using the best conventional numerical methods he could find, Tuncer Cebeci of McDonnell-Douglass corporation computed the longest solution yet, well past the time of the flow in the picture above, and found no singularity. He summarized his frustration in a scientific journal as:
We contend that [...] there is no justification for the claim of Sears and Telionis that [the boundary layer equations] can develop a singularity at a finite T[ime] and that, on the contrary, solutions exist for all T[ime].Cebeci was right in that there was no singularity in the time range he computed, even though previous authors had said there was. But this did not mean that there would not be one for a still later time.
Meanwhile, my PhD advisor Shan-fu Shen and I had been following
a very different approach.
We divided the air around the cylinder
into small pieces and tracked the motion of each piece numerically.
This is called a Lagrangian approach, after the great eighteenth
century Italian mathematician Joseph Louis Lagrange.
It made it possible to continue the computation to longer times
than anybody else before, and we found a singularity.
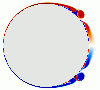
It occurred after the cylinder had moved over three quarters of a diameter.
Compare the previous picture at which the cylinder had moved over a distance
of half a diameter with the next one for a full diameter:
 (Click the picture to see a larger version of it).
(Click the picture to see a larger version of it).
We presented our results at a conference in Poland in 1977, and we submitted it to the reputed Journal of Fluid Mechanics, but it was flatly rejected. Not very encouraging for a young PhD student! I managed to convince Professor Shen that I really did know what I was doing and he send back a sharp reply, but to no avail. The editor himself replied:
They do not recommend rejection because of 'bad numerics', they do so because they do not find any sufficiently substantive contribution to understanding; and one of them suggests parenthetically that perhaps some discrepancies are due to the numerics.(A revised version was submitted to the Journal of Computational Physics and appeared in there 1980. Thirteen years later, the Journal of Fluid Mechanics published a two-part paper by Stephen Cowley and myself about the solution and its application to more general situations).
The first support for our computations came in 1979 from K. C. Wang, then at Martin Marietta corporation. Independently, he got results using a conventional numerical method that suggested a breakdown of the solution at roughly the same time that we computed. Unfortunately, his computation was not accurate enough to convince skeptical fluid dynamicists.
Another PhD student to the rescue! Stephen Cowley of England had been trying to address the same problem mathematically. Although there is no mathematical solution to the boundary layer equations, if certain approximations are made, mathematical solutions do become possible. And mathematicians have been developing very clever ways to improve such approximations until almost no error is left. Using such souped-up approximations, Stephen found that the solution range seemed to be terminating at exactly the point at which Shan-fu Shen and I had experienced our singularity. We exchanged notes, Stephen cursed a lot (he wanted to be the first to make the discovery!), but since the numerical solution and the mathematical one were exactly the same, there was really not much doubt left.
Since that time, other authors have re-computed the flow and verified these results using other, more conventional, numerical methods. I still believe that, if you don't know when and where the singularity occurs, a well-conducted Lagrangian computation is the only truly reliable method. Yet a Lagrangian computation is much more difficult than the usual computational procedures, and it has not yet become really popular. A small band of pioneers is working to change this, and one day, all of our computational points may move just as the air does.
 Return
to my home page.
Return
to my home page.Prandtl, L. (1904) Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Ludwig Prandtl gesammelte Abhandlüngen, volume 2. Springer-Verlag 1961. (The `father of boundary layer theory.' Best graduate student: Theodore Von Karman.) Return
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit kleiner Reibung. Zeitschrift für Mathematik und Physik 56, 1-37. (Student of Prandtl.) Return
Moore, F. K. (1958) On the separation of the unsteady laminar boundary layer. In Boundary-Layer Research, ed. H.G. Gortler. Springer. (Among others, he is a professor at Cornell University, where I got my PhD.) Return
Sears, W. R. & Telionis, D. P. (1975) Boundary-layer separation in unsteady flow. SIAM Journal on Applied Mathematics 23, 215. (The work was performed at Cornell University. This was Telionis' 1971 PhD thesis, under Sears. Sears was the best student of Theodore Von Karman, and is also an experienced pilot.) Return
Goldstein, S. (1948) On laminar boundary-layer flow near a position of separation. Quarterly Journal of Mechanics and Applied Mathematics 1, 43-69. Return
Cebeci, T. (1979) The laminar boundary layer on a circular cylinder impulsively started from rest. Journal of Computational Physics 31, 153-172. (Also a professor at Cal State at Long Beach.) Return
Van Dommelen, L. L. & Shen, S. F. (1980) The spontaneous generation of the singularity in a separating laminar boundary layer. Journal of Computational Physics 38, 125-140. Return
Wang, K. C. (1979) Unsteady boundary-layer separation. Martin Marietta Laboratory, Baltimore, Maryland, Technical Report MML TR 79-16c. (Now a professor at the University of California at San Diego.) Return
Cowley, S. J. (1983) Computer extension and analytic continuation of Blasius expansion for impulsive flow past a circular cylinder. Journal of Fluid Mechanics 135, 389-405. Return
Ingham, D. B. (1984) Unsteady separation. Journal of Computational Physics 53, 90-99.
Henkes, R. A. W. M. & Veldman, A. E. P. (1987) On the breakdown of the steady and unsteady interacting boundary-layer description. Journal of Fluid Mechanics 179, 513-530. (From the Netherlands, where I was born.)
Riley, N. & Vasantha, R. (1989) Unsteady high-Reynolds-number flows. Journal of Fluid Mechanics 205, 243-262.
Puppo, G. (1990) PhD Thesis, Courant Institute, New York.
Christov, C. I. & Tzankov, I. T. (1993) Numerical investigation of the laminar boundary layer flow around an impulsively moved circular cylinder. Computer Methods in Applied Mechanics and Engineering 109, 1-15.
Cowley, S. J., Hocking, L. M. & Tutty, O. R. (1985) The stability of solutions of the classical unsteady boundary-layer equation. Physics of Fluids A 28, 441-443. Return