| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
3.5.6.1 Solution pipee-a
Question:
Plug the mass of an electron, 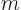
 9.109 38 10
9.109 38 10 kg, and the rough size of an hydrogen atom, call it
kg, and the rough size of an hydrogen atom, call it 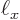
 2 10
2 10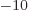 m, into the expression for the ground state kinetic energy and see how big it is. Note that
m, into the expression for the ground state kinetic energy and see how big it is. Note that 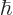
 1.054 57 10
1.054 57 10 J s. Express in units of eV, where one eV equals 1.602 18 10
J s. Express in units of eV, where one eV equals 1.602 18 10 J.
J.
Answer:
or 9.4 eV. The true value is about 4.5 eV. That is in the ball park.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
