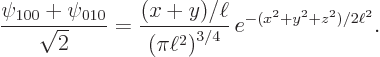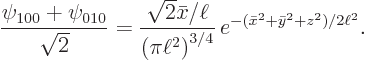| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.1.5.1 Solution harme-a
Question:
Just to check that this book is not lying, (you cannot be too careful), write down the analytical expression for  and
and 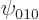 using table 4.1. Next write down
using table 4.1. Next write down 

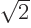 and
and 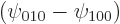

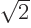 . Verify that the latter two are the functions
. Verify that the latter two are the functions  and
and 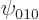 in a coordinate system
in a coordinate system 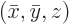 that is rotated 45 degrees counter-clockwise around the
that is rotated 45 degrees counter-clockwise around the 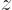 -axis compared to the original
-axis compared to the original 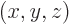 coordinate system.
coordinate system.
Answer:
Take the rotated coordinates to be 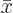 and
and 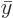 as shown:
as shown:
A vector displacement of magnitude  in the
in the  -direction has a component along the
-direction has a component along the 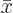 -axis of magnitude
-axis of magnitude 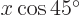 , equivalent to
, equivalent to 

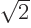 . Similarly, a vector displacement of magnitude
. Similarly, a vector displacement of magnitude  in the
in the  -direction has a component along the
-direction has a component along the 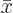 -axis of magnitude
-axis of magnitude 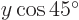 , equivalent to
, equivalent to 

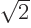 . So in general, for any point
. So in general, for any point  ,
,
Similarly you get
Turning now to the eigenfunctions, taking the generic expression
and substituting 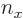
 1,
1, 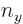

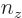
 0, you get
0, you get
Now substitute for  and
and  from table 4.1:
from table 4.1:
where the constant 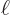 is as given in table 4.1. You can multiply out the exponentials:
is as given in table 4.1. You can multiply out the exponentials:
The same way, you get
So, the combination 

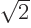 is
is
Now 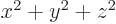 is according to the Pythagorean theorem the square distance from the origin, which is the same as
is according to the Pythagorean theorem the square distance from the origin, which is the same as 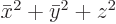 . And since
. And since 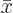



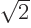 , the sum
, the sum 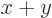 in the combination eigenfunction above is
in the combination eigenfunction above is  . So the combination eigenfunction is
. So the combination eigenfunction is
which is exactly the same as  above, except in terms of
above, except in terms of 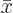 and
and 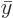 . So it is
. So it is  in the rotated frame.
in the rotated frame.
The other combination goes the same way.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![\begin{displaymath}
\begin{picture}(200,200)(-100,-100)\thinlines
\put(-100,0...
...ar x$}}
\put(-64,60){\makebox(0,0)[rt]{$\bar y$}}
\end{picture}\end{displaymath}](img285.gif)
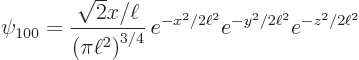


![]()
![]()
![]()