| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.1.4.3 Solution harmd-c
Question:
Write down the explicit expression for the eigenstate 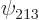 using table 4.1, then verify that it looks like figure 4.2 when looking along the
using table 4.1, then verify that it looks like figure 4.2 when looking along the 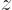 -axis, with the
-axis, with the  -axis horizontal and the
-axis horizontal and the  -axis vertical.
-axis vertical.
Answer:
The generic expression for the eigenfunctions is
and substituting 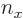
 2,
2, 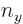
 1 and
1 and 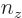
 3, you get
3, you get
Now substitute for those functions from table 4.1:
where the constant 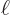 is as given in table 4.1.
is as given in table 4.1.
The first polynomial within square brackets in the expression above is zero at 

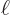

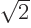 and
and 


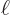

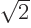 , producing the two vertical white lines along which there is zero probability of finding the particle. Similarly, the second polynomial within square brackets is zero at
, producing the two vertical white lines along which there is zero probability of finding the particle. Similarly, the second polynomial within square brackets is zero at 
 0, producing the horizontal white line. Hence looking along the
0, producing the horizontal white line. Hence looking along the 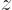 -direction, you see the distribution:
-direction, you see the distribution:
Figure 4.2:
Energy eigenfunction 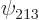 .
.
![\begin{figure}\centering {}
\setlength{\unitlength}{1pt}
\begin{picture}(300,21...
...{3}}
\put(-31,107){\makebox(0,0)[t]{$-\ell /\sqrt 2$}}
\end{picture}\end{figure}](img276.gif) |
Seen from above, you would see four rows of three patches, as the third polynomial between brackets produces zero probability of finding the particle at 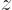

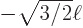 ,
, 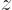
 0, and
0, and 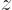

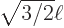 , splitting the distribution into four in the
, splitting the distribution into four in the  -direction.
-direction.
This example illustrates that there is one more set of patches in a given direction each time the corresponding quantum number increases by one unit.
![]()
![]() -
-![]() -
-![]() -
-![\begin{displaymath}
\psi_{213} = {\displaystyle\frac{[2(x/\ell)^2-1][2y/\ell][2(...
...ht)^{3/4}}} e^{-x^2/2\ell^2}e^{-y^2/2\ell^2}e^{-z^2/2\ell^2}
\end{displaymath}](img274.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() -
-![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]() -
-