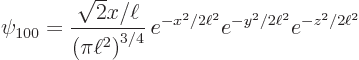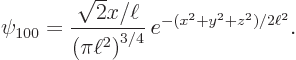| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.1.2.4 Solution harmb-d
Question:
Write out the eigenstate  fully.
fully.
Answer:
Taking the generic expression
and substituting 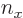
 1,
1, 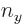

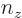
 0, you get
0, you get
Now substitute for 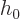 and
and 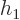 from table 4.1:
from table 4.1:
where the constant 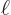 is as given in table 4.1. You can multiply out the exponentials:
is as given in table 4.1. You can multiply out the exponentials:
![]()