| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.4.2.2 Solution esdb-b
Question:
Continuing the previous question, what are the standard deviations in energy, square angular momentum, and 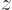 angular momentum?
angular momentum?
Answer:
Since the expectation value in energy is 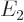 , as are the eigenvalues of each state, the standard deviation is zero.
, as are the eigenvalues of each state, the standard deviation is zero.
This is expected since every measurement produces 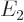 ; there is no deviation from that value.
; there is no deviation from that value.
Similarly the standard deviation in 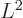 is zero:
is zero:
For the 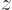 angular momentum, the expectation value is zero but the two states have eigenvalues
angular momentum, the expectation value is zero but the two states have eigenvalues 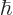 and
and 
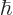 , so
, so
Whether 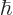 or
or 
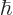 is measured, the deviation from zero has magnitude
is measured, the deviation from zero has magnitude 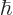 .
.
![]()
![]() ,
,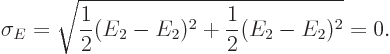
![]()
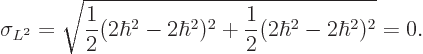
![]()
![]()
![]()
![]() ,
,