| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.3.5 Solution dot-e
Question:
Verify that  is not a normalized function on the interval 0
is not a normalized function on the interval 0 


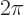 , and normalize it by dividing by its norm.
, and normalize it by dividing by its norm.
Answer:
Since  is not one,
is not one,  is not a normalized function on 0
is not a normalized function on 0 


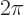 . If you divide by its norm, i.e. by
. If you divide by its norm, i.e. by  , however,
, however,
![]()
![]()
![]()
![]()
![]() ,
,
