| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.2.2.3 Solution angub-c
Question:
Actually, based on the derived eigenfunction,  , would any macroscopic particle ever be at a single magnetic quantum number in the first place? In particular, what can you say about where the particle can be found in an eigenstate?
, would any macroscopic particle ever be at a single magnetic quantum number in the first place? In particular, what can you say about where the particle can be found in an eigenstate?
Answer:
The square magnitude of the wave function gives the probability of finding the particle. The square magnitude,
is independent of  . So to be in a state of definite angular momentum, the particle must be at all sides of the axis with equal probability. A macroscopic particle will at any given time be at a single angle compared to the axis, not at all angles at once. So, a macroscopic particle will have indeterminacy in angular momentum, just like it has indeterminacy in position, linear momentum, energy, etcetera.
. So to be in a state of definite angular momentum, the particle must be at all sides of the axis with equal probability. A macroscopic particle will at any given time be at a single angle compared to the axis, not at all angles at once. So, a macroscopic particle will have indeterminacy in angular momentum, just like it has indeterminacy in position, linear momentum, energy, etcetera.
Since the probability distribution of an eigenstate is independent of  , it is called
, it is called axisymmetric around the 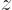 -axis
-axis
. Note that the wave function itself is only axisymmetric if 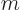
 0, in other words, if the angular momentum in the
0, in other words, if the angular momentum in the 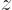 -direction is zero. Eigenstates with different angular momentum look the same if you just look at the probability distribution.
-direction is zero. Eigenstates with different angular momentum look the same if you just look at the probability distribution.
![]() ,
,![]() ,
,![]() -
-![]()
![]()
![]() -
-