| Partial Differential Equations 0.15 alpha |
|
© Leon van Dommelen |
|
5.7 Finding the Green's functions
We can, if we want, write the solution for  in other ways that may
be more efficient numerically. The solution was, rewritten more
concisely in terms of the eigenvalues and eigenfunctions:
in other ways that may
be more efficient numerically. The solution was, rewritten more
concisely in terms of the eigenvalues and eigenfunctions:
The first part is due to the inhomogeneous term 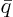 in the partial differential equation,
the second due to the initial condition
in the partial differential equation,
the second due to the initial condition
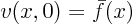
Look at the second term first, let's call it  ,
,
We can substitute in the orthogonality relationship for  :
:
and change the order of the terms to get:
We define a shorthand symbol for the term within the square brackets:
Since this does not depend on what function  is, we can evaluate
is, we can evaluate
 once and for all. For any
once and for all. For any  , the corresponding temperature
is then simply found by integration:
, the corresponding temperature
is then simply found by integration:
Function 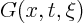 by itself is the temperature
by itself is the temperature 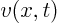 if
if  is
a single spike of heat initially located at
is
a single spike of heat initially located at 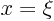 . Mathematically,
. Mathematically,
 is the solution for
is the solution for  if
if  is the ``delta function''
is the ``delta function''
 .
.
Now look at the first term in  , due to
, due to 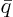 , let's call it
, let's call it 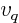 :
:
We plug in the orthogonality expression for
 :
:
and rewrite
We see that
where the function  is exactly the same as it was before.
However,
is exactly the same as it was before.
However,
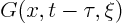 describes the temperature due to a spike
of heat added to the bar at a time
describes the temperature due to a spike
of heat added to the bar at a time  and position
and position  ;
it is called the Green's function.
;
it is called the Green's function.
The fact that solving the initial value problem ( ), also
solves the inhomogeneous partial differential equation problem (
), also
solves the inhomogeneous partial differential equation problem (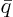 ) is known as the Duhamel
principle. The idea behind this principle is that function
) is known as the Duhamel
principle. The idea behind this principle is that function 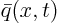 can be ``sliced up'' as a cake. The contribution of each
slice
can be ``sliced up'' as a cake. The contribution of each
slice
 of the cake to the solution
of the cake to the solution  can be
found as an initial value problem with
can be
found as an initial value problem with
 as the
initial condition at time
as the
initial condition at time  .
.
![]() in other ways that may
be more efficient numerically. The solution was, rewritten more
concisely in terms of the eigenvalues and eigenfunctions:
in other ways that may
be more efficient numerically. The solution was, rewritten more
concisely in terms of the eigenvalues and eigenfunctions:
![\begin{displaymath}
v(x,t) = \sum_n
\left[
\int_{\tau=0}^t \bar q_n(\tau)
...
...\tau
+ \bar f_n e^{-\kappa \lambda_n t}
\right]
X_n(x).
\end{displaymath}](img1177.gif)
![]() ,
,
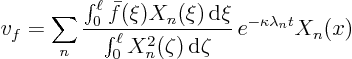
![\begin{displaymath}
v_f = \int_0^\ell
\left[
\sum_n
\frac{X_n(\xi) X_n(...
...ta}
e^{-\kappa \lambda_n t}
\right]
\bar f(\xi) d \xi
\end{displaymath}](img1182.gif)
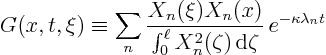
![]() , due to
, due to ![]() , let's call it
, let's call it ![]() :
:
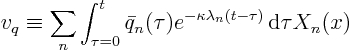
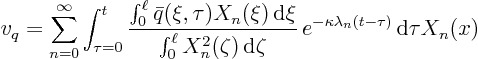
![\begin{displaymath}
v_q = \int_{\tau=0}^t \int_0^\ell
\left[
\sum_n
\fra...
...-\tau)}
\right]
\bar q(\xi,\tau) { \rm d}\xi {\rm d}\tau
\end{displaymath}](img1192.gif)
![]() ), also
solves the inhomogeneous partial differential equation problem (
), also
solves the inhomogeneous partial differential equation problem (![]() ) is known as the Duhamel
principle. The idea behind this principle is that function
) is known as the Duhamel
principle. The idea behind this principle is that function ![]() can be ``sliced up'' as a cake. The contribution of each
slice
can be ``sliced up'' as a cake. The contribution of each
slice
![]() of the cake to the solution
of the cake to the solution ![]() can be
found as an initial value problem with
can be
found as an initial value problem with
![]() as the
initial condition at time
as the
initial condition at time ![]() .
.