3.6 First order equations in more dimensions

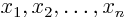The procedures of the previous subsections extend in a logical way to more dimensions. If the independent variables are $x_1,x_2,\ldots,x_n$ , the first order quasi-linear partial differential equation takes the form

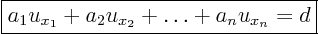$\begin{displaymath} \fbox{$\displaystyle a_1 u_{x_1} + a_2 u_{x_2} + \ldots + a_n u_{x_n} = d $} % \end{displaymath}$

(3.6)

where the

and

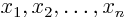may depend on $x_1,x_2,\ldots,x_n$ and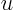

The characteristic equations can now be found from the ratios

$\begin{displaymath} \fbox{$\displaystyle {\rm d}x_1 : {\rm d}x_2 : \ldots : {\rm d}x_n : {\rm d}u = a_1 : a_2 : \ldots : a_n : d $} % \end{displaymath}$

(3.7)

After solving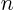

different ordinary differential equations from this set, the integration constant of one of them, call it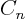

can be taken to be a general

-parameter function of the others,

$\begin{displaymath} C_n=C_n(C_1,C_2,\ldots,C_{n-1}) \end{displaymath}$

and then substituting for $C_1,C_2,\ldots,C_{n-1}$ from the other ordinary differential equation, an expression for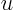

results involving one still undetermined,

parameter function

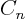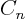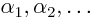To find this remaining undetermined function, plug in whatever initial condition is given, renotate the parameters of to $\alpha_1,\alpha_2,\ldots$ and express everything in terms of them to find function $C_n(\alpha_1,\alpha_2,\ldots)$ .