| A New Mesh-Free Vortex Method |
|
Shankar Subramaniam |
|
6.2 Numerical implementation of diffusion
In this section we describe the numerical implementation of the new
redistribution method formulated in section 4.1.
Basically, the redistribution method is a matter of finding the fractions
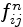 from the system of linear equations (4.8) and following,
and redistributing the circulation of the each vortex according
to these fractions.
Assuming that valid fractions
from the system of linear equations (4.8) and following,
and redistributing the circulation of the each vortex according
to these fractions.
Assuming that valid fractions 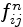 exist, they are found
using linear programming techniques, as explained in subsections
6.2.1 and 6.2.2 below.
However, it is possible that no valid fractions exist
using the available vortices in a neighborhood.
In that case, we create new vortices until there is a solution, see
subsection 6.2.3.
Further, due to convection effects, some vortices may move sufficiently
close to another vortex that they are no longer useful for
computational purposes. In subsection 6.2.4, we discuss
how to remove those vortices. Also, near the edges of a diffusing region,
the vorticity is exponentially small. To avoid excessive vortices, some
cut-off strength is needed below which vortices are ignored. However,
choosing this cut-off can be quite tricky, as we will explain
in subsection 6.2.5.
Finally, in subsection 6.2.6 we
discuss evaluating the vorticity to compare with analytical solutions and
other numerical computations in the literature.
exist, they are found
using linear programming techniques, as explained in subsections
6.2.1 and 6.2.2 below.
However, it is possible that no valid fractions exist
using the available vortices in a neighborhood.
In that case, we create new vortices until there is a solution, see
subsection 6.2.3.
Further, due to convection effects, some vortices may move sufficiently
close to another vortex that they are no longer useful for
computational purposes. In subsection 6.2.4, we discuss
how to remove those vortices. Also, near the edges of a diffusing region,
the vorticity is exponentially small. To avoid excessive vortices, some
cut-off strength is needed below which vortices are ignored. However,
choosing this cut-off can be quite tricky, as we will explain
in subsection 6.2.5.
Finally, in subsection 6.2.6 we
discuss evaluating the vorticity to compare with analytical solutions and
other numerical computations in the literature.
Subsections
![]() from the system of linear equations (4.8) and following,
and redistributing the circulation of the each vortex according
to these fractions.
Assuming that valid fractions
from the system of linear equations (4.8) and following,
and redistributing the circulation of the each vortex according
to these fractions.
Assuming that valid fractions ![]() exist, they are found
using linear programming techniques, as explained in subsections
6.2.1 and 6.2.2 below.
However, it is possible that no valid fractions exist
using the available vortices in a neighborhood.
In that case, we create new vortices until there is a solution, see
subsection 6.2.3.
Further, due to convection effects, some vortices may move sufficiently
close to another vortex that they are no longer useful for
computational purposes. In subsection 6.2.4, we discuss
how to remove those vortices. Also, near the edges of a diffusing region,
the vorticity is exponentially small. To avoid excessive vortices, some
cut-off strength is needed below which vortices are ignored. However,
choosing this cut-off can be quite tricky, as we will explain
in subsection 6.2.5.
Finally, in subsection 6.2.6 we
discuss evaluating the vorticity to compare with analytical solutions and
other numerical computations in the literature.
exist, they are found
using linear programming techniques, as explained in subsections
6.2.1 and 6.2.2 below.
However, it is possible that no valid fractions exist
using the available vortices in a neighborhood.
In that case, we create new vortices until there is a solution, see
subsection 6.2.3.
Further, due to convection effects, some vortices may move sufficiently
close to another vortex that they are no longer useful for
computational purposes. In subsection 6.2.4, we discuss
how to remove those vortices. Also, near the edges of a diffusing region,
the vorticity is exponentially small. To avoid excessive vortices, some
cut-off strength is needed below which vortices are ignored. However,
choosing this cut-off can be quite tricky, as we will explain
in subsection 6.2.5.
Finally, in subsection 6.2.6 we
discuss evaluating the vorticity to compare with analytical solutions and
other numerical computations in the literature.