2.2 Quan­tum me­chan­ics

Schrödinger, in his fa­mous equa­tion, as­so­ci­ated en­ergy with the par­tial time dif­fer­en­ti­a­tion op­er­a­tor, and lin­ear mo­men­tum with the par­tial space dif­fer­en­ti­a­tion op­er­a­tor in a given di­rec­tion:

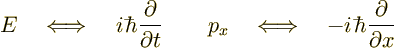$$E\quad\Longleftrightarrow\quad i\mathchoice {{\textstyl... ...mu h}{{}^{{\rm -}}\mkern-12mu h}\frac{\partial}{\partial x} %$$ (2.3)

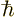Here $\mathchoice {{\textstyle{}^{{\rm -}}\mkern-9mu h}}{{}^{{\rm -}}\mkern-9mu h} {{}^{{\rm -}}\mkern-12mu h}{{}^{{\rm -}}\mkern-12mu h}$ is the scaled Planck’s con­stant and 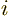$i$ is $\sqrt{-1}$.

The above re­sults are of crit­i­cal im­por­tance for this pa­per, be­cause the Mi­ata-light in­ter­ac­tion is due to ex­change of the en­ergy and mo­men­tum of pho­tons of light. There­fore, it is help­ful to make the above re­la­tions spe­cific for pho­tons:

$$E = \mathchoice {{\textstyle{}^{{\rm -}}\mkern-9mu h}}{{}... ...}}\mkern-12mu h}{{}^{{\rm -}}\mkern-12mu h}\frac{\omega}{c} %$$ (2.4)

These ex­pres­sions are known as the Planck-Ein­stein and de Broglie re­la­tions. They may be de­rived by ap­ply­ing Schrödinger’s as­so­ci­a­tions on a com­plex, prop­a­gat­ing mono­chro­matic light wave. As is well known, the first ex­pres­sion is con­sis­tent with Ein­stein’s re­la­tion (2.1) in view of the fact that pho­tons have zero rest mass.