EML 3002L M.E. Tools Lab 10/08/19
MATLAB Exam 1 Van Dommelen 12:30-1:45 pm

NO CELL PHONES, HEADPHONES/BUDS, NO CALCULATORS. SAVE FREQUENTLY. SAVE BEFORE PUBLISHING!!!

ONLY MATLAB MAY BE ACTIVE ON YOUR COMPUTER. Acrobat may only be open at the end, when you are ready except for publishing and actively looking at exam1q1.pdf, exam1q2.pdf, or exam1q3.pdf with it.

VARIABLE NAMES MUST BE APPROPRIATE AND CLEARLY SHOW WHAT VARIABLE IT IS OR A 50% CREDIT REDUCTION IS APPLIED. USE THE SAME NAMES AS IN THE QUESTION.

After translation into mathematics, only MATLAB may be used to solve the full problem as posed. Use the appropriate procedures as covered in the lectures.

Open notes: print-outs of lectures and homeworks allowed. You can also use your own homework .m files.

1. The objective in this question is to solve the equation
   
   $$1 - e^{-t} - t e^{-t} = S$$
   
   
   for the time $t$, given a value of $S$.

   The equation above determines the time $t$ it takes for a car wheel that rolls off a step down of size $S$ to hit the ground behind the step. In particular the left hand side is the distance traveled downwards by the wheel before it hits the ground after the step, and the right hand side is the total size of the step down.

   Define a function that can be used by fzero to find the time $t$ at which the equation above is satisfied for given $S$. The function should work unchanged for any value of $S$, so do not set a value for $S$ inside the function. Call the function Distance, as surely you recognize that it is really the vertical distance $d$ between the wheel and the ground behind the step.

   Make sure your function allows input argument $t$ to be an array instead of a scalar.

   Now plot this function using 51 $t$ values from 0 to 5, for the two values of $S$ equal to 0.25 and 0.75. Use a grid.

   Use mark-up comments to explain why the interval from 0 to 5 will work for sure in both cases to find the time $t$ that the wheel reaches the ground.

   Then find the two times using fzero using that interval and print them out as

      For S = 1.12, t = *.123456 (interval [1 1]).

   where the star means whatever digits MATLAB want to print out, and 12... is a count of digits to output. Absolutely no data numbers inside the FORMATSTRING, just format descriptors.

   Make sure that you change FUNNAME or Blah into Distance in the header of q1.m before publishing! Careful: do not mess up the format of the two lines involved while doing this!

   Solution Grading

2. The Clausius-Clapeyron equation of thermodynamics relates the changes of the pressure $P$ and the temperature $T$ in the two phase region of a substance as:
   
   $$\frac{{\rm d}P}{{\rm d}T} = \frac{s_{\rm {fg}}}{v_{\rm {fg}}}$$
   
   
   That means that if we integrate the ratio $s_{\rm {fg}}/v_{\rm {fg}}$ with respect to the temperature $T$, we should get the pressure change.

   Below is an extract of the saturated data of water given in the Sonntag book:
   

   $$\begin{array}{rrrr} T & P &v_{\rm fg}&s_{\rm fg}\\ 5 & 0... ...57.789 & 8.3706 \\ 25 & 3.169 & 43.358 & 8.1905 \end{array}$$
   
   
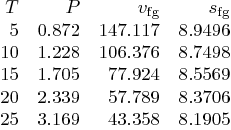
   Copy this table as is into your solution in q2.m and then find the integrand $s_{\rm {fg}}/v_{\rm {fg}}$ at the 5 temperatures.

   Spline interpolate this integrand at 101 plot temperatures from 5 to 25. Then plot the 5 values of the integrand against the 5 temperatures as little black circles, and the spline interpolate as a red broken (dashed) line. Use title “Clausius-Clapeyron Integrand”, axis labels T and sfg/vfg, use a grid, and a legend tabulated,” “spline interpolate placed in the bottom right of the plot. Let MATLAB choose the horizontal axis limits, but force it to use a vertical axis from 0 to 0.2.

   Finally, integrate the spline interpolate from temperature 5 to 25 and compare the pressure difference between 5 and 25 that you get this way with the exact pressure difference that you get from the above table.

   Also integrate the linear interpolate and compare that with exact.

   Solution Grading

3. Chemical engineers routinely deal with tough ordinary differential equations. As a toy example, consider the one-way reaction
   
   $$2 A + B \longrightarrow A_2B$$
   
   
   Each time the reaction occurs, it removes two $A$ and one $B$ and creates one new $A_2B$. So the differential equations governing the concentrations $[A]$, $[B]$, and $[A_2B]$ of $A$, $B$, and $A_2B$ respectively are
   

   $$\frac{{\rm d}[A]}{{\rm d}t} = -2r \qquad \frac{{\rm d}[B]}{{\rm d}t} = -r \qquad \frac{{\rm d}[A_2B]}{{\rm d}t} = r$$ (1)

   
   
   where $r$ is the reaction rate. Since two $A$ and one $B$ must come together for the reaction, the reaction rate can reasonably be assumed to be
   
   $$r = k [A]^2 [B]$$
   
   
   where $k$ is some constant that depends on at least temperature. Assume that the time $t$ is rescaled such as to make
   
   $$k=1$$
   
   

   Solve the above system of three ODE using ode45 for 101 times $t$ from 0 to 100. Use variable names cA, cB, and cA2B for $[A]$, $[B]$, and $[A_2B]$ respectively. Take the initial conditions to be that $[A]=0.25$, $[B]=0.25$, and $[A_2B]=0$.

   Call the function needed by ode45 A2BRates. Show in your first command in q3.m that help A2BRates explains what the function does and what its input and output arguments are.

   Plot the concentrations against time, using red for $[A]$, blue for $[B]$, and black for $[A_2B]$.

   Make sure that you change FUNNAME into A2BRates in the header of q3.m before publishing! Careful: do not mess up the format of the two lines involved while doing this!

   Solution Grading