solvesys.m (lowercase) that, assuming
that a matrix size 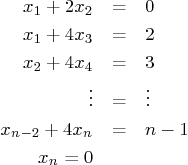
For example, if
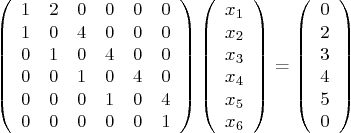
Script
solvesys.m should initialize the system matrix for loop over the interior equations. (Do not use special
matrices here. And the nonzero coefficients of the initial and
final equations should be done separately.) The final matrix and
right hand side vector should be printed out.
Then have Matlab check whether it will be able to find a reasonable solution to the system, and if not, display a message to that effect.
Otherwise let Matlab solve the system using the proper method, and print the solution. However, assuming that the right hand sides of the equations are measured values with a relative error of 0.001, let Matlab also estimate the relative error that that solution will have, and if it is greater than 5%, let Matlab print the following warning:
*** May have an error of *%using an appropriate
fprintf (no decimals in the percentage).
Your script should work for any reasonable value of exam2q1.m to test it out for
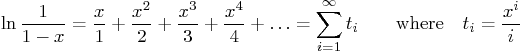
where
Your job is to write a script (being
examq2.m) that tries to
sum the above Taylor series in terms of (This relation could be improved upon, but we will keep it simple.) Before your summation solution, set variable
fprintf,
print out:
Total number of terms summed: *
The obtained value is 1.1234567890123456
The "exact" value is 1.1234567890123456
The difference between the two is 1.1E-12.
where for the exactvalue use
fprintf
FORMATSTRINGs.
- An unstable system has the Laplace transform solution
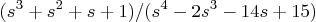
- To get an idea of the system properties, factor this ratio exactly. Your answer should take the form of a single ratio of multiplied factors.
- Find the exact partial fraction expansion.
- The equation of the normalized “Lemniscate of
Bernoulli” is:
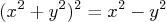
Let Matlab find the exact values of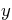 in terms of
in terms of  .
.
- Define the following symbolic function:
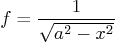
Next:- Let Matlab find the symbolic antiderivative
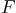 .
.
- Let Matlab exactly evaluate
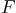 when
when 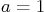 and
and
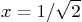
- Let Matlab convert
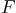 into a numerical function
into a numerical function
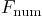 that evaluates the antiderivative numerically.
that evaluates the antiderivative numerically.
- Evaluate
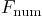 when the values 1 and
when the values 1 and 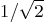 are substituted for
are substituted for 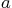 and
and  respectively. Print out this
value to 32 decimals behind the point using
respectively. Print out this
value to 32 decimals behind the point using fprintf. - Compare with the earlier exact value, printed out to 32 correct digits.
- Let Matlab find the symbolic antiderivative