| (1) | |||||
| (2) | |||||
| (3) | |||||
| (4) | |||||
| (5) | |||||
| (6) | |||||
| (7) |
Take
| (8) | |||||
| (9) | |||||
| (10) | |||||
| (11) | |||||
| (12) |
However, your code should still work correctly if you change
n) into a bigger value, without other changes.
Initialize the matrix of this system of equations to zeros, then use
a for loop over the equations to put in the nonzero elements.
Be careful with the first and last equations as they have a variable
out of order. Also create the right hand side vector. Print out
matrix and right hand sides as [A,b].
Use an if statement to check whether the system of equations
has a reasonably accurate solution. If it does, your code should
solve the system and print out the solution. If it does not, your
code should print an appropriate warning. This should again
continue to work for whatever value is given to variable n.
- Use
ezplotto plot the function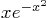 from
from 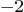 to 2. Turn on the grid.
to 2. Turn on the grid.
- Find the partial fraction expansion of the ratio
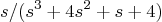
- For the quartic
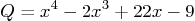
- Let Matlab find the exact roots, i.e. the exact four values
of
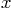 where
where 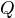 is zero.
is zero.
- Let Matlab factor the quartic
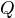 . Your result should take
the form of parenthetical expressions multiplied together.
. Your result should take
the form of parenthetical expressions multiplied together.
- Let Matlab find the derivative and antiderivative of the
quartic
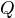 .
.
- Let Matlab find the exact integral of the quartic
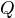 between the limits 0 and 2.
between the limits 0 and 2.
- Let Matlab find the exact roots, i.e. the exact four values
of
| 15 | 20 | 25 | 30 | 40 | 50 | 60 | 75 | 90 | |
| 60 | 105 | 175 | 255 | 430 | 670 | 940 | 1600 | 2100 |
Measured” and “Approximate, placed in the southeast corner. Use disp to comment on how well you think the fit is.